Лекальные Кривые.

Контуры некоторых машиностроительных деталей имеют сложную форму и состоят из линий различных видов: прямых, дуг окружностей и лекальных кривых.
На фигуре №145 показаны примеры таких деталей, в очертание которых частично или полностью входят лекальные кривые линии.

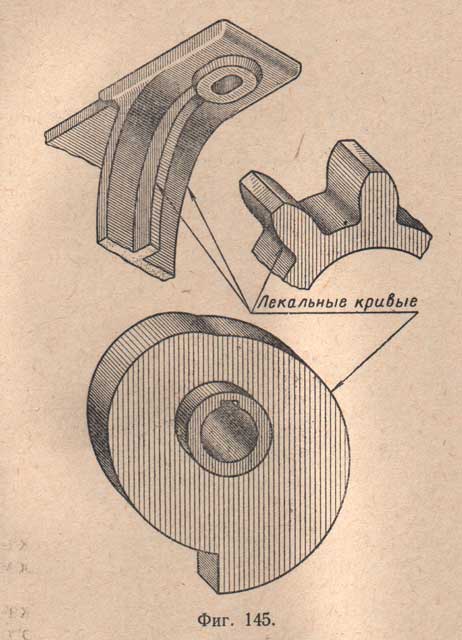
Лекальную кривую можно рассматривать как линию, состоящую из бесчисленного количества бесконечно малых дуг окружностей при постепенном изменении места их центров и радиусов кривизны. Пример приближенного очертания лекальной кривой показан на чертеже №146.

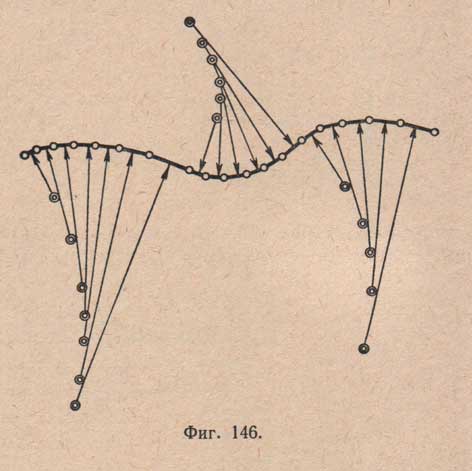
Для более точного изображения лекальной кривой необходимо мысленно бесконечно уменьшить длину каждой дуги, а следовательно, бесконечно увеличить количество дуг и их центров.
Такую кривую по причине бесконечно большого количества различных центров, радиусов и точек перехода невозможно вычертить при помощи циркуля; для ее вычерчивания необходимо прибегать к помощи лекал. Ниже приведены описания и построения некоторых лекальных кривых, которыми наиболее часто приходится пользоваться при выполнении машиностроительных чертежей. К таким кривым относятся: эллипс, парабола, гипербола, эвольвента окружности; спираль Архимеда, синусоида и циклические кривые: циклоида, эпициклоида, гипоциклоида.
Кривая, полученная при пересечении прямого кругового конуса наклонной плоскостью, пересекающей все его образующие (угол наклона секущей плоскости должен быть меньше угла наклона образующих), имеет очертание э л л и п с а (фиг.147, а).

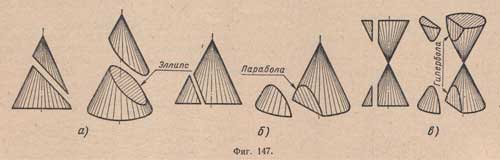
Кривая, полученная при пересечении прямого кругового конуса наклонной плоскостью, параллельной одной из образующих (угол наклона секущей плоскости должен быть равен углу наклона образующих), имеет очертание п а р а б о л ы (фиг.147, б).
Кривая, полученная при пересечении прямого кругового конуса плоскостью, параллельной двум образующим (угол наклона секущей плоскости должен быть больше угла наклона образующих), имеет очертание гиперболы (фиг.147, в).