Овал.
Овалом называется замкнутая выпуклая кривая, состоящая из двух основных дуг, плавно переходящих одна в другую при помощи одинаковых, симметрично расположенных, дуг перехода внутреннего касания. Если основные дуги проведены одинаковыми радиусами, то овал имеет две оси симметрии, а следовательно, и центр симметрии (фиг.180,а)
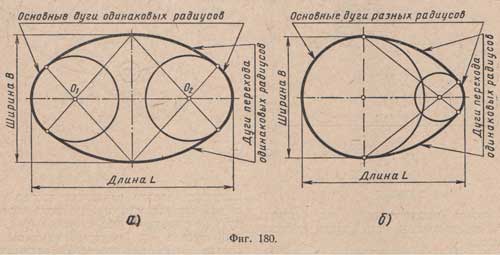
Если основные дуги проведены разными радиусами, то овал имеет только одну ось симметрии и называется овоидом (фиг.180,6).
Очерк овала и овоида относится к коробовым кривым. Коробовой кривой линией называется плоская кривая, состоящая из ряда сопряженных дуг окружностей.
Построение овала по заданным длине L = АВ и ширине В = CD. На (фиг.181,а) показано нахождение центра О1 основной дуги и центра О2 дуги перехода. Последовательность построения показана цифрами:
1 и 2 - проведение осей овала (АВ и CD);
3 - проведение наклонного отрезка СВ;
4 - проведение дуги BE;
5 - проведение дуги EF;
б, 7 и 8 - деление отрезка FB пополам и нахождение центров О1 и О2, причем центр О2 в зависимости от ширины В овала может находиться выше или ниже точки D или совпадать с ней.
На (фиг.181,б) показано нахождение центров О'1 основной дуги и О'2 - дуги перехода и вычерчивание основных дуг (из центров О1 и О'1) и дуг перехода (из центров О2 и О'2).
Последовательность построения показана цифрами:
9 - нахождение центра О'1;
10 - нахождение центра O'2;
11 - проведение луча из центра О2 через центр О'1;
12 - проведение луча из центра О'2 через центр О'1;
13 - проведение луча из центра О'2 через центр О1;
14 - проведение левой опорной дуги между лучами, проведенными из центров O2 и O'2 через центр O'1 точки К и Р пересечения лучей
дугой явятся точками перехода;
15 - аналогичное проведение правой опорной дуги и нахождение точек М и N перехода;
16 и 17 - проведение дуг перехода.
Смотри ещё: Эпициклоида











