Параллельные прямые.
Если прямые параллельны, то все их одноименные проекции на комплексном чертеже параллельны (фиг. 213,а).
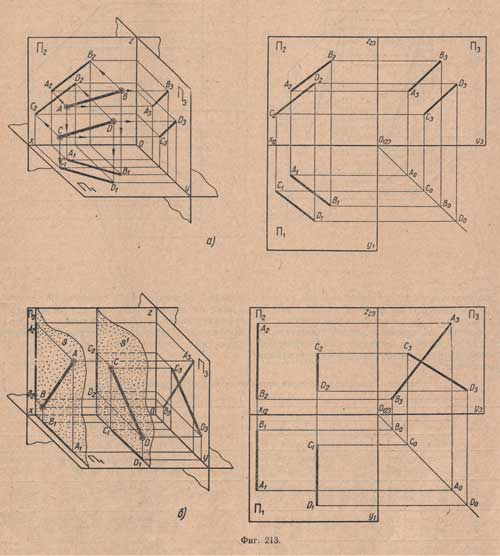
И наоборот, если все одноименные проекции прямых на комплексном чертеже параллельны, то и сами прямые параллельны. В большинстве случаев о параллельности прямых можно судить по двум данным проекциям, но есть исключение, когда о параллельности прямых по двум данным проекциям судить нельзя: когда две прямые параллельны одной из плоскостей проекций (фиг.213,б), например плоскости П3 (профильные прямые), то, рассматривая на комплексном чертеже только фронтальные и горизонтальные их проекции, нельзя судить о параллельности этих прямых, хотя одноименные фронтальные А2В2 и С2B2, а также одноименные горизонтальные А1В1 и C1D1 проекции прямых (в данном случае профильные) параллельны.
Отсюда заключаем, что для определения по комплексному чертежу взаимного положения горизонталей, фронталей и профильных прямых по двум данным проекциям (расположенным попарно параллельно осям проекций) необходимо построить их третьи проекции, по которым и определять взаимное положение прямых.











