Пересекающиеся прямые.
Если две прямые пересекаются, то все их одноименные проекции на комплексном чертеже пересекаются и точки пересечения любых двух проекций будут расположены на одной линии связи.
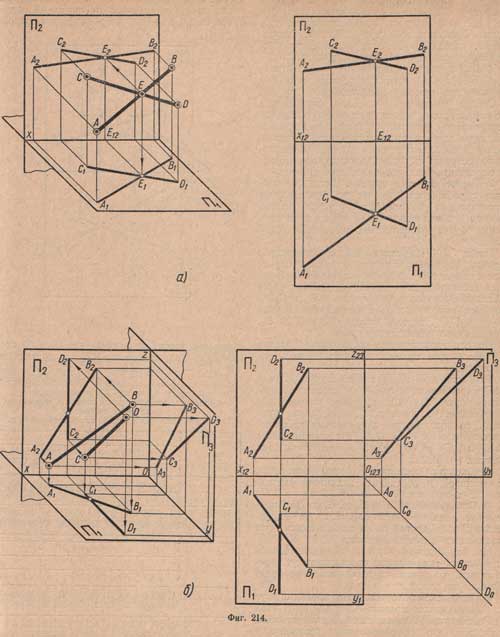
На (фиг.214,а) показаны две пересекающиеся прямые общего положения. В данном случае для суждения о взаимном расположении прямых достаточно двух проекций, так как одноименные фронтальные проекции А2В2 и C2D2, так же как и одноименные горизонтальные А1В1 и C1D1, пересекаются в точках Е1 и E2, лежащих на одной линии связи.
Но есть исключение, когда нельзя судить о пересечении прямых по двум данным их проекциям.
Так, если одна из двух данных прямых (или обе) параллельна к одной из плоскостей проекций (фиг.214,б), например прямая CD параллельна плоскости П3 (профильная прямая), то при наличии одноименных проекций фронтальных А2В2 и C2D2 и горизонтальных А1В1 и C1D1 нельзя судить о пересечении двух данных прямых.
Необходимо построить третью проекцию, по которой и определить взаимное положение двух прямых.











