Проектирование многоугольников.
При проектировании плоских фигур, ограниченных прямыми линиями, достаточно спроектировать лишь вершины данной фигуры и затем последовательно соединить их одноименные проекции прямыми линиями; в результате получим проекции всех сторон фигуры, т. е. проекции данной фигуры.
Требуется спроектировать треугольник, заданный координатами вершин А, В и С. Спроектируем вершины А, В и С треугольника, как точки, получим их проекции А1В1С1 и А2В2С2 (фиг.243,а). Соединим одноименные проекции точек прямыми, получим проекции А1В1, В1С1, С1А1 и А2В2, В2С2, С2А2 сторон треугольника, т.е. проекции A1B1C1 и А2В2С2 заданного треугольника (фиг.243,б).
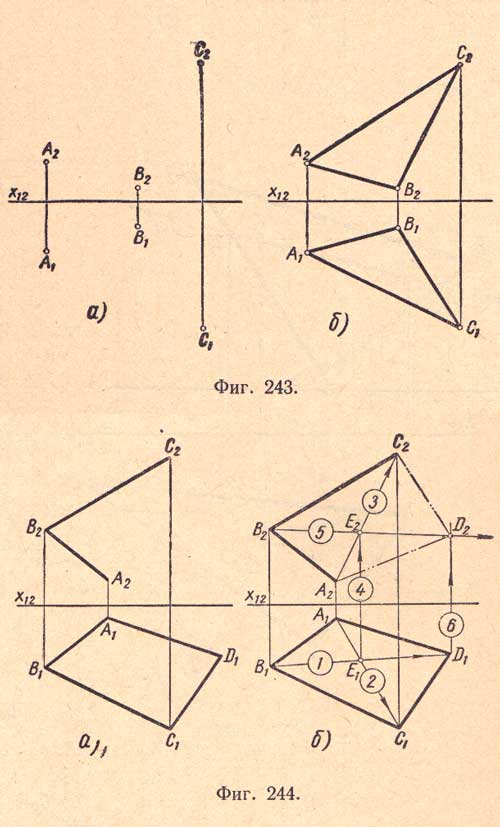
Треугольник всегда является плоской фигурой, чего нельзя сказать про четырехугольник, пятиугольник и т.д., плоскостность которых надо выявлять на чертеже.
Требуется спроектировать плоский четырехугольник ABCD (фиг.244,а), заданный горизонтальной проекцией (А1В1С1D1) и фронтальной проекцией двух смежных сторон АВ и ВС (A2B2, В2С2)
Решение задачи сводится к нахождению фронтальной проекции вершины D (D1,D2).
Воспользуемся для данного случая двумя пересекающимися прямыми (диагоналями), определяющими плоскость фигуры четырехугольника ABCD.
Порядок построения фронтальной проекции показан цифрами:
1, 2 - провести горизонтальные проекции диагоналей B1D1 А1С1;
3 - провести фронтальную проекцию диагонали А2С2;
4 - найти фронтальную проекцию Е2 (точки пересечения диагоналей);
5 - провести прямую через точки В2 и E2 (направление второй диагонали);
6 - найти фронтальную проекцию D2 Найденную точку D2 соединяем прямыми с одноименными проекциями вершин С и А (С2 и А2), получим недостающие проекции A2D2 и D2С2 сторон АО и ОС четырехугольника (фиг.244,б). Четырехугольник ABCD плоский, так как его вершины лежат на пересекающихся прямых, которыми определяется плоскость.
Плоская фигура может занимать различные положения по отношению к плоскостям проекций:
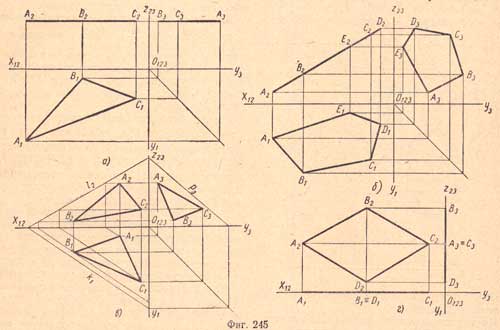
а) быть параллельной одной из плоскостей проекций (фиг.245,а);
б) быть перпендикулярной к одной из плоскостей проекций и наклонной к двум другим (фиг.245,б);
в) быть наклонной к трем плоскостям проекций (фиг.245,б);
г) лежать в одной из плоскостей проекций (фиг.245,г).
В случае «а» фигура будет расположена в горизонтальной, фронтальной или профильной плоскостях. По свойству этих плоскостей одна из проекций равна натуральной величине проектируемой фигуры как лежащая в плоскости, параллельной плоскости проекций, а две другие проекции прямые, сливающиеся с проекциями плоскости, которая является двояко-проектирующей.
В данном случае горизонтальная проекция треугольника AВС (A1B1C1) равна его натуральной величине. Фронтальная проекция - прямая, сливающаяся с проекцией λ2 (фиг.245,а).
В случае «б» фигура будет расположена в горизонтально-, фронтально- или профильно - проектирующих плоскостях. По свойству этих плоскостей одна из проекций явится прямой, сливающейся с соответствующей проекцией проектирующей плоскости; две другие проекции не представляют ее натуральной величины, так как фигура расположена в плоскости, находящейся под углом к плоскостям проекций.
Фронтальная проекция пятиугольника выявлена прямой, сливающейся с проекцией δ2; горизонтальная проекция - фигура, не равная натуральной величине проектируемого пятиугольника (фиг.245,б).
В случае «в» фигура будет расположена в плоскости общего положения, по свойству этой плоскости все проекции выявятся фигурами, не представляющими натуральной величины фигуры. Фронтальная, горизонтальная и профильная проекции — треугольники, не равные величине проектируемого треугольника (фиг.245,в).
В случае «г» фигура будет расположена в плоскостях проекции П1 или П2, или П3. Тогда одна из проекций будет сливаться с самой фигурой и равна ей; две другие проекции - прямые, сливающиеся с осями проекций, так как фигура расположена в плоскости проекций. Фронтальная проекция ромба сливается с ромбом; горизонтальная и профильная проекции сливаются с осями проекций х и у (фиг.245,г).
Технические рисунки правильных многоугольников.....











