Прямая и точка в плоскости.
Прямая лежит в плоскости, если она имеет с плоскостью две общие точки. Пусть дана плоскость двумя прямыми (фиг.232,а), например параллельными AВ и CD (A1B1; А2В2 и C1D1; C2D2). Требуется в заданной плоскости провести прямую.
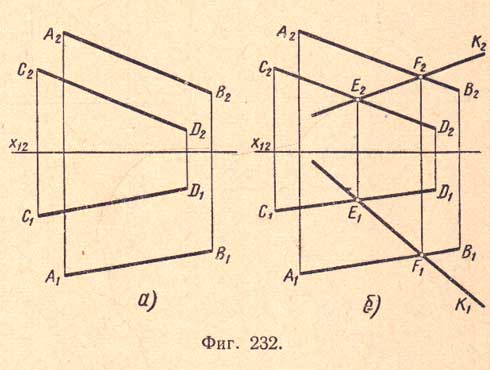
Чтобы прямая лежала в данной плоскости, необходимо, чтобы эта прямая имела с плоскостью две общие точки, которые и определят эту прямую.
Возьмем на данных прямых две произвольно расположенные точки Е и F (Е1Е2 и F1F2) и проведем через них прямую k (k1 и k2). Эта прямая будет расположена в данной плоскости, так как она имеет с ней две общие точки (фиг.232,б).
Изображение на комплексном чертеже прямой, расположенной в плоскости, заданной следами:
а) Возьмем на следах k и L произвольно точки М (М1 М2) и N (N1 N2) как следы прямой (фиг.233,а).
б) Проведем через одноименные фронтальные (М2 и N2) и горизонтальные (М1 и N1) проекции точек М и N прямые (фиг.233,б).
Прямая MN будет расположена в плоскости а как имеющая с ней две общие точки.
Отсюда следует: для того чтобы прямая принадлежала плоскости, надо, чтобы следы прямой лежали на одноименных следах этой плоскости.
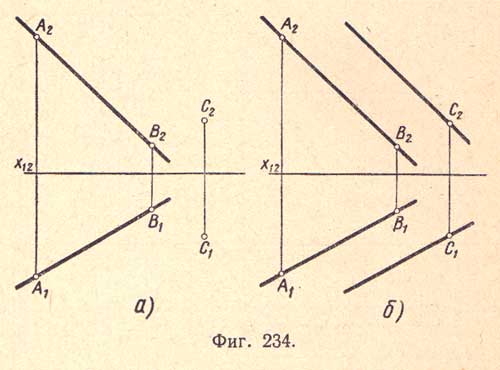
Прямая лежит в плоскости, если имеет с ней одну общую точку и параллельна прямой, лежащей в плоскости. Пусть задана плоскость (фиг.234,а) прямой АВ (А1В1 и A2В2) и точкой С (C1C2).
Требуется в заданной плоскости провести прямую через заданную точку С.
Проведем через точку С (С1С2) прямую параллельно прямой АВ (А1В1 и А2В2); эта прямая будет расположена в данной плоскости, так как она имеет с плоскостью общую точку и параллельна прямой, лежащей в данной плоскости (фиг.234,б).
Изображение на комплексном чертеже прямой, расположенной в плоскости и параллельной одному из следов плоскости. Для проведения прямой в заданной следами плоскости а общего положения (прямая должна быть параллельна горизонтальному следу k данной плоскости), возьмем на следе L произвольную точку N (N1N2) как точку, лежащую в данной плоскости а (фиг.235,а).
След k принимаем за прямую, лежащую в плоскости П1 Проведем прямую через точку N1 параллельно прямой k1 получим горизонтальную проекцию h1 прямой h. Фронтальная проекция h2 прямой h пройдет через точку N2 и расположится параллельно оси х12 как прямая, параллельная плоскости П1 (фиг.235,б).
Прямая h будет принадлежать плоскости а, как имеющая с ней общую точку (след N) и параллельная прямой (следу к), лежащей в данной плоскости.
Аналогичное построение будет справедливо и для случая, когда требуется провести прямую в заданной следами плоскости общего положения параллельно фронтальному следу L (фиг.235,в и г).
Прямая h, лежащая в плоскости а, параллельная горизонтальной плоскости проекций П1, называется горизонталью данной плоскости (фиг.235,а и б).
Прямая f, лежащая в плоскости а, параллельная фронтальной плоскости проекций П2, называется фронталью данной плоскости (фиг.235,в и г).
Отсюда следует, что через всякую точку, лежащую в данной плоскости, можно провести одну горизонталь и одну фронталь. Разобрав различные изображения прямой в плоскости, можно на комплексном чертеже решить обратную задачу, т. е., имея проекции прямой, провести через нее соответствующую плоскость.
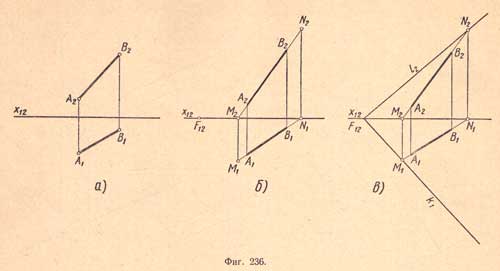
Пример 1.Через данный отрезок АВ (А1В1 А2В2) провести плоскость общего положения и показать проекции следов этой плоскости (фиг. 236,а).
Зная, что следы прямой должны лежать на одноименных следах плоскости, сначала находим следы прямой, затем выбираем в произвольном месте на оси х12 точку F12 схода следов (фиг. 236,б) и, наконец, проводим следы плоскости общего положения (фиг. 236,в).
Пример 2.Через данный отрезок АВ (А1В1, А2В2) провести горизонтально - проектирующую плоскость и показать ее проекцию.
Так как в этом случае горизонтальная проекция прямой должна сливаться с горизонтальной проекцией плоскости, проводим горизонтальную проекцию σ1 плоскости через горизонтальную проекцию прямой (фиг. 237).
Точка в плоскости. В случае изображения на комплексном чертеже проекций точки, лежащей в данной плоскости, сначала проводят в плоскости вспомогательную прямую, а затем на ней изображают точку.
а) Построить проекции произвольной точки A, принадлежащей плоскости а, заданной следами (фиг.238,а).
Воспользуемся фронталью данной плоскости а как прямой, лежащей в плоскости. Спроектируем одну из фронталей плоскости а, например f (f1, f2) (фиг.238,б).
Затем на фронтали проектируем произвольную точку, которую принимаем за заданную точку А (А1A2) (фиг.238,в).
Так как обе проекции А1 и А2 точки А лежат на проекциях фронтали f плоскости а, то, следовательно, точка А лежит в заданной плоскости а.
Таким же способом можно выполнить построение, воспользовавшись горизонталью h (фиг.238,г)
б) Пусть плоскость задана двумя пересекающимися прямыми АВ (A1B1, A2A2) и ВС (B1C1, В2С2), требуется найти проекции D1 и D2 точки D лежащей в заданной плоскости вне этих прямых (фиг.239,а). Зная, что проекции точки должны лежать на проекциях прямой, принадлежащей данной плоскости, проводим вспомогательную прямую EF (E1F1, E2F2) так, чтобы она лежала в данной плоскости (фиг.239,б). Затем на прямой EF (фиг.239,в) проектируем точку D (D1D2).
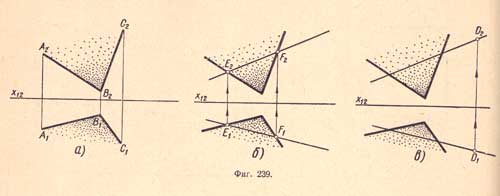
Так как точка D (D1D2) лежит на прямой EF (E1F1, E2F2), находящейся в заданной плоскости, следовательно, она принадлежит заданной плоскости.
в) Пусть плоскость σ задана фронтальной проекцией σ2. Требуется построить проекции произвольной точки А, принадлежащей данной плоскости.
Так как плоскость σ - фронтально - проектирующая, то по свойству проектирующих плоскостей фронтальная проекция точки, лежащей в этой плоскости, должна сливаться с фронтальной проекцией данной плоскости.
Спроектируем произвольную точку А так, чтобы фронтальная проекция A2 точки лежала на проекции σ2, это и определит, что точка A (A1A2) лежит в заданной плоскости (фиг.240).
Такое построение будет справедливо и для остальных проектирующих плоскостей.
Рассмотрим несколько примеров.
Пример I. Дан треугольник AВС (А1В1С1, A2B2C2) и произвольно расположенная точка D (фиг.241,а); требуется определить, лежит ли точка D (D1D2) в плоскости данного треугольника? Порядок проверки указан цифрами на (фиг.241,б).
1 - проводим через точки С2 и D2 прямую, получаем точку K2;
2 - проводим вертикальную линию связи, получаем точку К1;
3 - проводим через точки С1 и К1 прямую; в данном случае она прошла через точку Ьъ следовательно, точка D (D1 D2) лежит на прямой СК (С1К1, С2K2), так как ее проекции лежат на проекциях этой прямой и на одной линии связи; прямая СК принадлежит плоскости треугольника ABC (A1B1C1, А2В2С2), так как имеет с ней две общие точки; следовательно, точка D принадлежит плоскости треугольника.
Пример II. Дан треугольник ABC и расположенная произвольно прямая EF (Е1F1 E2F2), требуется определить, лежит ли прямая в плоскости данного треугольника (фиг.242,а)?
Порядок проверки указан цифрами на (фиг.242,б):
1 - продолжаем отрезок E2F2; в пересечении с прямыми В2А2 и А2С2 получаем точки Р2 и Т2;
2 - проводим через точки Р2 и Т2 вертикальные линии связи до пересечения с прямыми В1А1 и А1С1 получаем точки Р1 и Т1;
3 - проведем через точки Р1 и T1 прямую; в данном случае прямая сливается с отрезком E1F1 следовательно, прямая РТ принадлежит плоскости треугольника, так как одноименные проекции точек Р и Т лежат на одноименных проекциях прямых ВА и АС, принадлежащих треугольнику, и на одной линии связи; следовательно, прямая EF принадлежит плоскости данного треугольника.
Проектирование многоугольников.....











