Синусоида.
Синусоидой называется кривая, изображающая постепенное изменение тригонометрической функции - синуса в - зависимости от постепенного изменения величины угла (фиг.168).
Прямая А'0А'12 называется осью синусоиды; точки А'3 и А'9 называются вершинами синусоиды; точки А'0 и А'6 и А'12 - точками перегиба, L - длина волны, равная А'0А'12 (если L - nD, то синусоида называется нормальной; если L > nD, то - вытянутой, если L < nD - сжатой).
Величина D называется амплитудой синусоиды.
Построение синусоиды.
Проводят вспомогательную окружность диаметром, равным данной амплитуде D, и на продолжении центровой линии отмечают отрезок L, равный заданной длине волны (фиг.169,а). Окружность делят на некоторое количество, например на 12, равных частей.
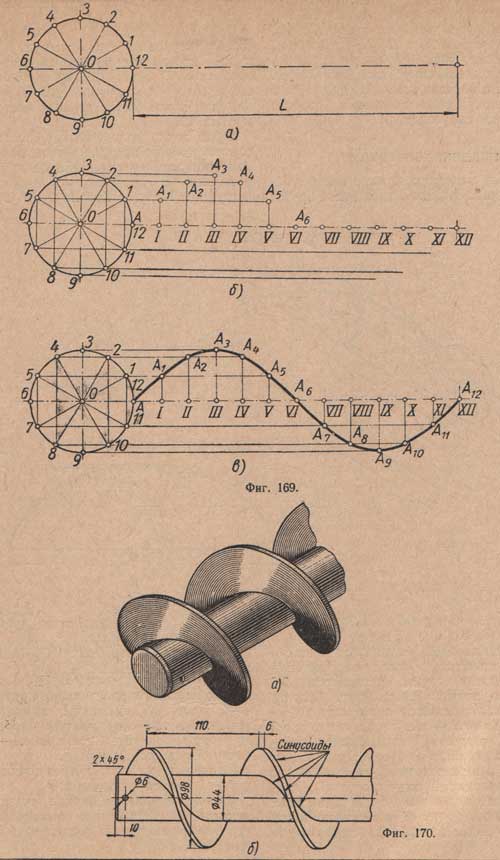
Отрезок L делят на столько же равных частей, на сколько была разделена окружность (фиг.169,б); из точек деления окружности проводят прямые параллельно оси синусоиды, а из точек I, II, III, IV и V - перпендикуляры к оси до пересечения с соответствующими прямыми - получают точки A1, A2, A3, A4, A5.
Аналогичным путем находят точки A7, A8, A9, A10, A12 (точки A, A6 и A12 лежат на оси), через полученные точки проводят кривую, которая явится искомой синусоидой (фиг.169,в).
На (фиг.170,а) показан шнек. На (фиг.170,б) дан чертеж шнека, часть очертания которого выполняется по синусоиде.
Далее: Эвольвента окружности.....











