Точка на трех плоскостях.

Изображение точки на трех плоскостях (на комплексном чертеже).
Придя к выводу, что две проекции точки вполне определяют ее положение в пространстве, все-таки следует заметить, что предметы имеют три измерения и что изображение предметов на чертеже получается более наглядным, а понимание чертежа значительно уясняется, если добавить третью проекцию на плоскость, перпендикулярную к первым двум (П₁ и П₂).
Пусть плоскости проекций П₁ и П₂ пересечены вертикальной плоскостью, перпендикулярной к ним (фиг.194,а), тогда пространство будет разделено на восемь частей, называемых октантами, а плоскости образуют восемь прямоугольных трехгранных углов.

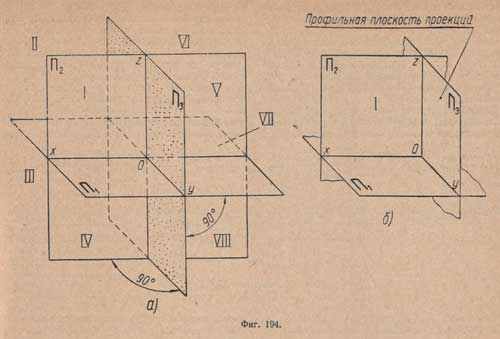
Новая плоскость пересечет плоскость П₁ по прямой, называемой осью проекций и обозначаемой буквой у, а плоскость П₂ - по прямой, называемой осью проекций и обозначаемой буквой z.
В системе трех взаимно - перпендикулярных плоскостей новую плоскость будем называть профильной плоскостью проекций и обозначать П₃.
В дальнейшем проектировать будем только в первом трехгранном углу (фиг.194,б).
Спроектируем точку А, расположенную в первом углу пространства (фиг.195 а). Для этого через точку А проведем проектирующие прямые, перпендикулярные к плоскостям проекций П₁ П₂ и П₃, точки пересечения которых с плоскостями явятся проекциями данной точки А (А₁, А₂, А₃).
Прямую АА₃, проектирующую точку А на плоскости П₃, будем называть профильно - проектирующей прямой, а проекцию П₃ - профильной проекцией точки. Расстояние точки А от плоскости П₃ будем называть широтой точки.
Проведем через проектирующие прямые АА₁ - АА₃ и АА₂ - АА₃ проектирующие плоскости (фиг.195,б).
Плоскость AA₂ A₂₃ A₃ перпендикулярна плоскостям проекций П₂ и П₃ и пересекает их по прямым А₂ А₂₃ и А₂₃ А₃, перпендикулярным к оси Z.
Плоскость АА₃ А₁₂ А₁ перпендикулярна плоскостям проекций П₁ и П₃ и пересекает их по прямым А₁ А₁₃ и А₁₃ А₃, перпендикулярным к оси у.
Для получения плоского чертежа точки А плоскость П₂ оставим неподвижной, а плоскости П₁ и П₃ будем вращать вокруг соответствующих осей проекций в направлении, указанном на чертеже стрелками (фиг.195,б), до совмещения с плоскостью П₂.

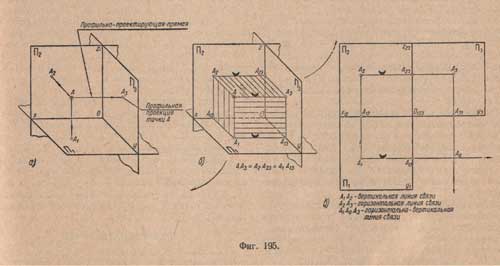
Рассматривая комплексный чертеж точки А на трех плоскостях, замечаем, что фронтальная и горизонтальная проекции точки А лежат на вертикальной линии связи А₂ А₁ (ранее нам знакомой, см.фиг.192,г). Фронтальная и профильная проекции лежат на прямой А₂ А₃, перпендикулярной к оси проекций z₂₃; такую прямую будем называть горизонтальной линией связи.
Горизонтальная проекция точки лежит на горизонтальной прямой, перпендикулярной к оси у₁, профильная проекция - на вертикальной прямой, перпендикулярной к оси у₃. При продолжении эти прямые пересекутся в точке А₀, такую ломаную линию будем называть горизонтально-вертикальной линией связи (фиг.195,е).
Построение профильной проекции точки может быть выполнено несколькими способами:
а) проводят ось z₂₃ (ее расстояние от проекции А₂ произвольно), затем из точки А₂ проводят горизонтальную линию связи и на ней от точки А₂₃ откладывают расстояние, равное А₁ А₁₂, получают искомую профильную проекцию А₃ (фиг.196,а);

б) построение аналогично предыдущему, за исключением того, что взамен откладывания расстояния A₁ A₁₂ проводят горизонтально - вертикальную линию связи, воспользовавшись вспомогательной дугой, проведенной из центра О₁₂₃ радиусом O₁₂₃ A_y (фиг.196,б);
в) построение аналогично предыдущему с той разницей, что вспомогательная дуга заменена вспомогательной прямой, проведенной из точки А_У под углом 45° (фиг.196,в);
г) построение аналогично предыдущему с той разницей, что взамен вспомогательной наклонной прямой, проведенной из точки А_У, проводим из точки О₁₂₃ вспомогательную наклонную прямую под углом 45° (фиг.196,г). Последний способ (г) наиболее удобен при работе чертежным прибором, поэтому в дальнейшем все построения указаны с применением этого способа.

Положения точки по отношению к плоскостям.....