Винтовые линии.
Цилиндрическая винтовая линия
К боковой поверхности прямого кругового цилиндра (стержня) подведен конец резца, принимаем его за точку А (фиг.363,а).
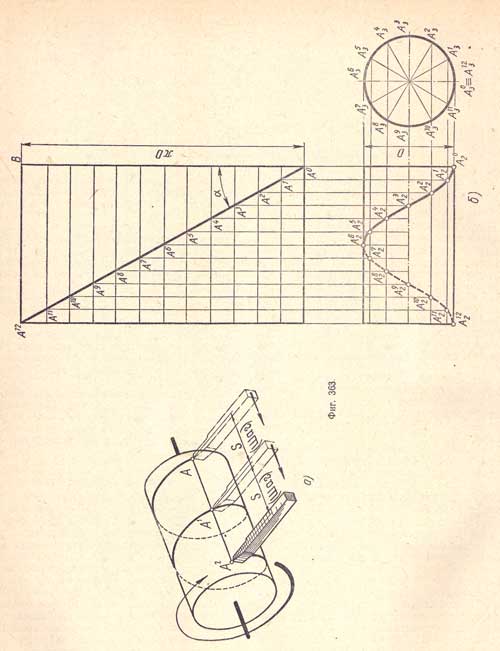
Придадим одновременно резцу равномерно поступательное движение, параллельное оси цилиндра, а цилиндру - равномерно вращательное, вокруг его оси, в результате конец резца, т. е. точки А, оставит на поверхности цилиндра пространственную кривую линию (риску), называемую цилиндрической винтовой линией.
После одного оборота цилиндра точка А - конец резца - переместится в точку А1 и образует часть винтовой линии, называемую витком. Расстояние АА1 = А1А2, измеряемое по образующей цилиндра, равняется шагу винтовой линии. Цилиндрическая винтовая линия, являясь пространственной кривой, может быть изображена на плоскости только своими проекциями (фиг.363,б).
Так как фронтальной проекцией цилиндрической винтовой линии является синусоида, то построение фронтальной проекции винтовой линии можно выполнить, как построение синусоиды, предварительно разделив окружность - профильную проекцию основания цилиндра - и отрезок A122 A02, равный шагу, отложенный на фронтальной проекции оси цилиндра, на одинаковое число равных частей, например на 12 (построение синусоиды см. на фиг.169).
Профильной проекцией цилиндрической винтовой линии является окружность, сливающаяся с профильной проекцией кругового цилиндра, так как все образующие цилиндра перпендикулярны плоскости П3.
Для построения проекций винтовой линии достаточно иметь размер диаметра цилиндра и величину шага.
Развертка винтовой линии осуществляется вместе с разверткой боковой поверхности цилиндра, на которой она нанесена и выявится прямой линией.
Развернем боковую поверхность цилиндра в плоскость, получим прямоугольник. Сторону, равную ПD, делим на 12 равных частей и через точки деления проводим образующие, а затем с фронтальной проекции переносим точки A02, A12,A22...,A122 на соответствующие образующие. Проведенная через полученные точки прямая А0 А12 будет разверткой одного витка винтовой линии.
Заметим, что прямая А0А12, являющаяся гипотенузой прямоугольного треугольника, наклонена под одним углом ко всем образующим цилиндра. Угол α называется углом подъема винтовой линии.
Построенная винтовая линия на (фиг.364), а является правой, так как на фронтальной проекции точка А, образующая винтовую линию, перемещается снизу слева вверх направо. В противном случае винтовая линия будет левой (фиг.364,б).
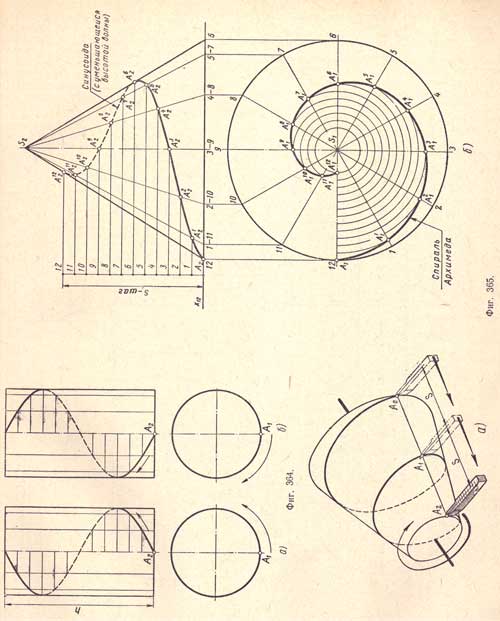
Коническая винтовая линия
К боковой поверхности прямого кругового конуса подведен конец резца, примем его за точку А0 (фиг.365,a). Придадим одновременно резцу равномерно - поступательное движение, а конусу равномерно - вращательное вокруг его оси; в результате конец резца, т.е. точка А0, оставит на поверхности конуса пространственную кривую линию - риску называемую конической винтовой линией. Аналогично цилиндрической коническая винтовая линия может быть как правого, так и левого направления.
На (фиг.365,б) показано построение проекций конической винтовой линии: окружность - горизонтальную проекцию основания конуса - и шаг h делим на одинаковое число равных частей, например на 12. Наносим на проекции конуса 12 образующих и, пользуясь делениями шага, находим на фронтальных проекциях соответствующих образующих точки A2, А12, А22, . . ,A122; соединив найденные точки плавной кривой, получим фронтальную проекцию конической винтовой линии - «затухающую» кривую с уменьшающейся высотой волны.
Горизонтальной проекцией является спираль Архимеда, ее построение видно из чертежа.











