Вращение плоскости вокруг ее следов.

Вращение плоскостей вокруг их следов, как осей, есть частный случай способа вращения. Следы плоскостей являются одними из множества горизонталей и фронталей данной плоскости.
В результате вращения плоскости вокруг горизонтального следа - горизонтали - все точки совмещаемой плоскости совместятся с горизонтальной плоскостью проекций, а в результате вращения плоскости вокруг фронтального следа - фронтали все точки плоскости совместятся с фронтальной плоскостью проекций. Такое действие - называют совмещением (фиг.265).

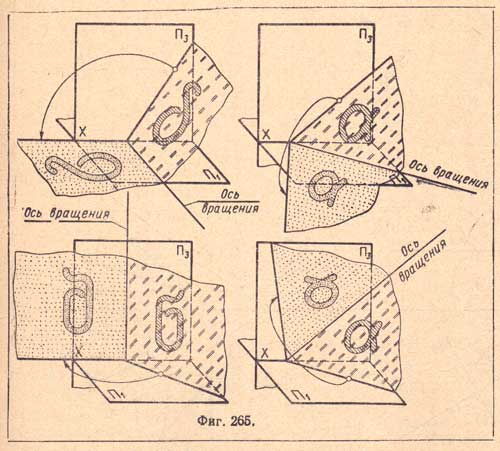
Каждый из следов плоскости является осью вращения, и, следовательно, все точки вращаемой плоскости описывают окружности в плоскостях, перпендикулярных к следу, вокруг которого происходит вращение.
1. Совмещение плоскости общего положения а с плоскостью П₁. Для решения этой задачи надо совместить любую точку следа i с плоскостью П₁ например точку А (фиг.266,а).

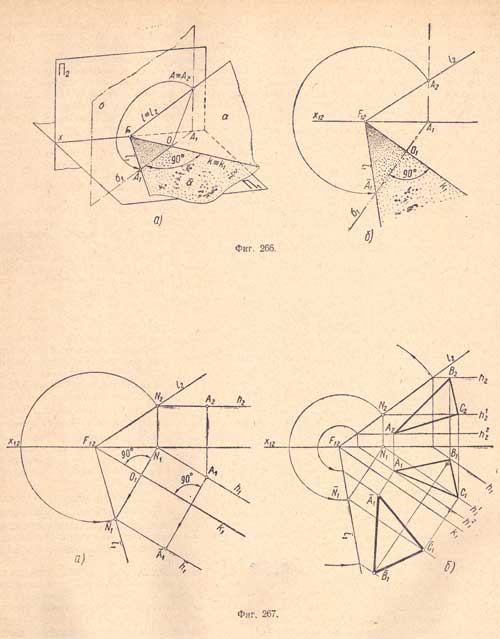
След k является осью вращения. Точка F схода следов лежит на оси вращения и не изменит своего положения.
Вводим плоскость вращения δ для точки А, перпендикулярную к следу k; она будет горизонтально - проектирующей и пересечет след k в точке О - центре вращения.
Радиусом вращения является отрезок ОА - линия пересечения плоскостей а и δ.
Точка А при вращении опишет в плоскости δ дугу и на проекции δ₁ определит место совмещенной точки А₁, через которую из точки F должен проходить совмещенный след i₁.
Рассмотрим, как выполнить на комплексном чертеже совмещение следа i с плоскостью П₁, (фиг.266,б).
На следе i оерут произвольную точку А (A₁ A₂) Затем через проекцию А₁ этой точки проводят проекцию δ₁ горизонтально - проектирующей плоскости δ перпендикулярно к проекции k₁ следа k, который принят за ось вращения.

Так как отрезок A₂F₁₂ при вращении плоскости не изменит своей величины, то точку ‾А₁ можно получить как пересечение проекции δ₁ с дугой, проведенной из центра F₁₂ радиусом F₁₂A₂.
Прямая, проведенная из точки F₁₂ через точку ‾А₁ является следом ‾i₁ совмещенным с плоскостью П₁ что и определяет совмещение плоскости а с плоскостью П₁.
В случае совмещения данной плоскости с плоскостью проекций П₂ следует в качестве плоскости вращения брать фронтально - проектирующую плоскость, перпендикулярную к следу i.

2. Совмещение точки, принадлежащей плоскости общего положения, с плоскостями проекций. Требуется совместить плоскость общего положения β, заданную проекциями k₁ и i₂ ее следов, с находящейся на ней точкой А с плоскостью проекций П₁ (фиг.267,а). Для решения этой задачи воспользуемся горизонталью. Проведем через заданную точку А горизонталь h, совместим ее и след i с плоскостью П₁ при помощи точки N (следа горизонтали), одновременно принадлежащей как горизонтали, так и следу i. Получим проекцию ‾N₁ совмещенной точки N и проекцию ‾i₁ совмещенного следа i. Зная, что горизонтальные проекции горизонталей параллельны следу плоскости, в которой они лежат, проводим из точки ¯N₁ прямую параллельно следу k₁ получаем совмещенную горизонталь и на ней проведением из точки А₁ прямой, перпендикулярной к следу k₁ определяем место совмещенной точки ‾А. Точка пересечения этой прямой с совмещенной горизонталью является искомой совмещенной проекцией ‾А₁.
При определении длины отрезка прямой, лежащего в плоскости общего положения, достаточно совмещения его крайних точек с одной из плоскостей проекций, а при определении формы и размеров фигуры - совмещения ее вершин.
На (фиг.267,б) приведен пример определения формы и размеров треугольника при помощи горизонталей, проведенных через его вершины.
3. Совмещение проектирующих плоскостей с плоскостями проекций. Следы проектирующих плоскостей при пересечении с плоскостями проекций образуют в пространстве прямой угол. При совмещении проектирующих плоскостей с плоскостями проекции этот угол сохраняется.
На (фиг.268,а) показано совмещение фронтально - проектирующей плоскости δ с лежащим на ней пятиугольником ABCDE с плоскостью П₁ путем вращения вокруг горизонтального следа.

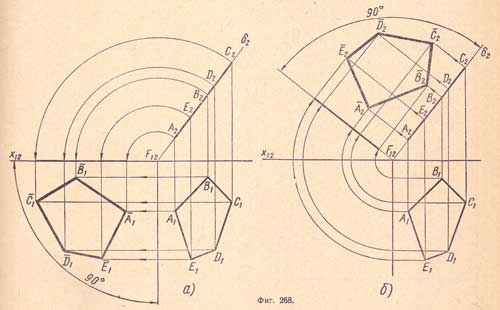
Фронтальная проекция δ₂ вместе с фронтальной проекцией пятиугольника совместится с осью х₁₂.
Горизонтальные проекции вершин - точки А₁, B₁, C₁, D₁, Е₁, - в то же время переместятся по прямым, параллельным оси х₁₂, на соответствующие расстояния и определят места проекции вершин совмещенного пятиугольника.
Соединив прямыми совмещенные проекции точек, получим проекцию совмещенного пятиугольника, по которой можно определить его форму, длину сторон, величину углов и его площадь.
На (фиг.268,б) показано совмещение фронтально - проектирующей плоскости δ с лежащим на ней пятиугольником с плоскостью П₂. В этом случае за ось вращения принята проекция δ₂.

Аксонометрические проекции.....