Призма.

Призмой называется многогранник, у которого две грани - равные многоугольники с соответственно параллельными сторонами, а все остальные грани - параллелограммы (фиг.282,а).

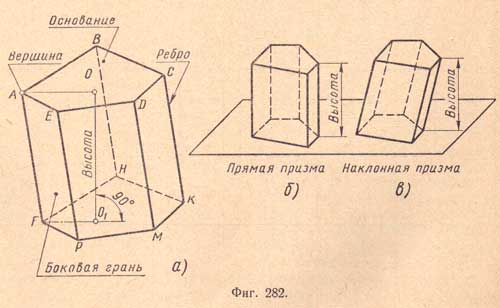
Многоугольники ABCDE и FHKMP, лежащие в параллельных плоскостях, называются основаниями призмы, перпендикуляр OO₁, опущенный из любой точки основания на плоскость другого, называется высотой призмы. Параллелограммы ABHF, BCKH и т.д. называются боковыми гранями призмы, а их стороны СК, DM и т.д., соединяющие соответственные вершины оснований, - боковыми ребрами. У призмы все боковые ребра равны между собой как отрезки параллельных прямых, заключенных между параллельными плоскостями.
Призма называется прямой (фиг.282,б) или наклонной (фиг.282,в) в зависимости от того, будут ли ее боковые ребра перпендикулярны или наклонны к основаниям. У прямой призмы боковые грани - прямоугольники. За высоту такой призмы можно принять боковое ребро.
Прямая призма называется правильной, если ее основания - правильные многоугольники. У такой призмы все боковые грани - равные прямоугольники.
Для изображения на комплексном чертеже призмы надо знать и уметь изображать элементы, из которых она состоит (точку, прямую, плоскую фигуру).
Анализ элементов правильной призмы и их изображение на комплексном чертеже (фиг.283, а - и)

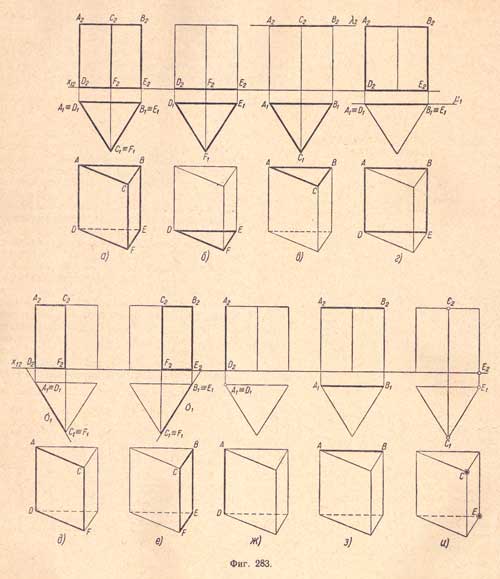
а) Комплексный чертеж призмы. Основание призмы расположено на плоскости проекций П₁; одна из боковых граней призмы параллельна плоскости проекций П₂.
б) Ниокнее основание призмы DEF - плоская фигура - правильный треугольник, расположенный в плоскости П₁; сторона треугольника DE параллельна оси х₁₂ - Горизонтальная проекция сливается с данным основанием и, следовательно, равна его натуральной величине; фронтальная проекция сливается с осью х₁₂ и равна стороне основания призмы.
в) Верхнее основание призмы АВС - плоская фигура - треугольник, расположенный в горизонтальной плоскости. Горизонтальная проекция сливается с проекцией нижнего основания и закрывает собой ее, так как призма прямая; фронтальная проекция - прямая, параллельная оси х₁₂, на расстоянии высоты призмы.
г) Боковая грань призмы ABED - плоская фигура - прямоугольник, лежащий во фронтальной плоскости. Фронтальная проекция - прямоугольник, равный натуральной величине грани; горизонтальная проекция - прямая, равная стороне основания призмы.
д) и е) Боковые грани призмы ACFD и CBEF - плоские фигуры - прямоугольники, лежащие в горизонтально - проектирующих плоскостях, расположенных под углом 60° к плоскости проекций П₂. Горизонтальные проекции - прямые, расположенные к оси х₁₂ под углом 60°, и равны натуральной величине сторон основания призмы; фронтальные проекции - прямоугольники, изображение которых меньше натуральной величины: две стороны каждого прямоугольника равны высоте призмы.
ж) Ребро AD призмы - прямая, перпендикулярная к плоскости проекций П₁. Горизонтальная проекция - точка; фронтальная - прямая, перпендикулярная оси х₁₂, равная боковому ребру призмы (высоте призмы).
з) Сторона АВ верхнего основания - прямая, параллельная плоскостям П₁ и П₂. Горизонтальная и фронтальная проекции - прямые, параллельные оси х₁₂ и равные стороне данного основания призмы. Фронтальная проекция отстоит от оси х₁₂ на расстоянии, равном высоте призмы.
и) Вершины призмы. Точка Е - вершина нижнего основания расположена на плоскости П₁. Горизонтальная проекция совпадает с самой точкой; фронтальная - лежит на оси x₁₂.Точка С - вершина верхнего основания - расположена в пространстве. Горизонтальная проекция имеет глубину; фронтальная - высоту, равную высоте данной призмы.
Отсюда следует: проектируя всякий многогранник, надо мысленно расчленить его на составные элементы и определить порядок их изображения, состоящий из последовательных графических операций. На (фиг.284 и фиг.285) приведены примеры последовательных графических операций при выполнении комплексного чертежа и наглядного изображения (аксонометрии) призм.
Изображение неправильной прямой пятиугольной призмы (фиг.284).

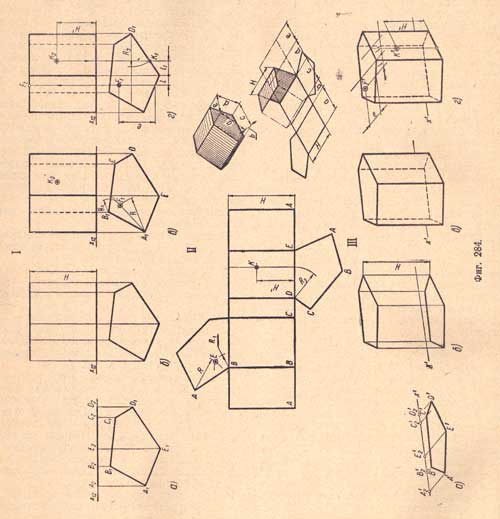
Дано:
1. Основание расположено на плоскости проекций П₁.
2. Ни одна из сторон основания не параллельна оси х₁₂.
I. Комплексный чертеж.
I, а. Проектируем нижнее основание - многоугольник, по условию лежащий в плоскости П₁.
I, б. Проектируем верхнее основание - многоугольник, равный нижнему основанию с соответственно параллельными нижнему основанию сторонами, отстоящий от нижнего основания на высоту H данной призмы.
I, в. Проектируем боковые ребра призмы - отрезки, расположенные параллельно; их горизонтальные проекции - точки, сливающиеся с проекциями вершин оснований; фронтальные - отрезки (параллельные), полученные от соединения прямыми одноименных проекций вершин оснований. Фронтальные проекции ребер, проведенные из проекций вершин В и С нижнего основания, изображаем штриховыми линиями, как невидимые.
I, г. Даны: горизонтальная проекция F₁ точки F на верхнем основании и фронтальная проекция К₂ точки К на боковой грани. Требуется определить места их вторых проекций.
Для точки F. Вторая (фронтальная) проекция F₂ точки F будет совпадать с проекцией верхнего основания, как точка, лежащая в плоскости этого основания; ее место определяется вертикальной линией связи.
Для точки К - Вторая (горизонтальная) проекция K₁ точки К будет совпадать с горизонтальной проекцией боковой грани, как точка, лежащая в плоскости грани; ее место определяется вертикальной линией связи.
II. Развертка поверхности призмы - плоская фигура, составленная из боковых граней - прямоугольников, у которых по две стороны равны высоте призмы, а другие две равны соответствующим сторонам основания, и из двух равных между собой оснований - неправильных многоугольников.
Натуральные размеры оснований и сторон граней, необходимые для построения развертки, выявлены на проекциях; по ним и производим построение; на прямой последовательно откладываем стороны АВ, ВС, CD, DE и ЕA многоугольника - основания призмы, взятые из горизонтальной проекции. На перпендикулярах, проведенных из точек А, В, С, D, Е и А, откладываем взятую из фронтальной проекции высоту Н данной призмы и через отметки проводим прямую. В результате получаем развертку боковых граней призмы.
Если к этой развертке пристроить основания призмы, получим развертку полной поверхности призмы. Основания призмы следует пристраивать к соответствующей боковой грани, пользуясь методом триангуляции.
На верхнем основании призмы при помощи радиусов R и R₁ определяем место точки F, а на боковой грани при помощи радиуса R₃ и Н₁ - точку K.
III. Наглядное изображение призмы в диметрии.
III, а. Изображаем нижнее основание призмы по координатам точек А, В, С, D и Е (фиг.284 I, a).
III, б. Изображаем верхнее основание параллельно нижнему, отстоящее от него на высоту Н призмы.
III, в. Изображаем боковые ребра, для чего соединяем прямыми соответствующие вершины оснований. Определяем видимые и невидимые элементы призмы и обводим их соответствующими линиями,
III, г. Определяем на поверхности призмы точки F и К - Точку F - на верхнем основании определяем при помощи размеров i и е; точку К - на боковой грани при помощи i₁ и H'.
Для изометрического изображения призмы и определения мест точек F и К следует придерживаться той же последовательности.
Изображение неправильной наклонной четырехугольной призмы (фиг.285).

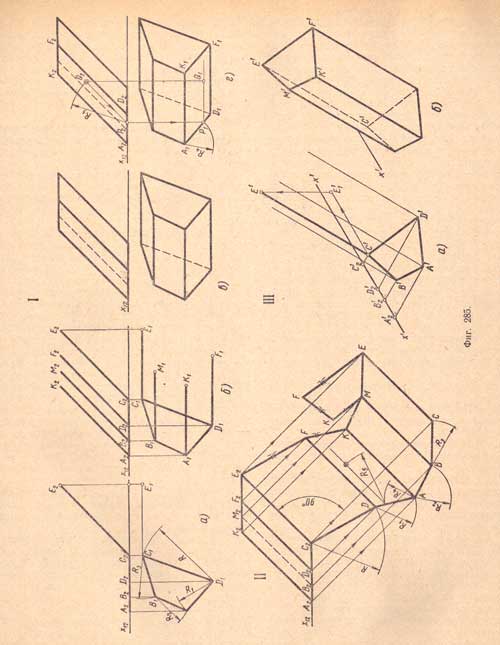
Дано:
1. Основание расположено на плоскости П₁.
2. Боковые ребра параллельны плоскости П₂.
3. Ни одна из сторон основания не параллельна оси x₁₂
I. Комплексный чертеж.
I, а. Проектируем по данному условию: нижнее основание - многоугольник, лежащий в плоскости П₁, и боковое ребро - отрезок, параллельный плоскости П₂ и наклонный к к плоскости П₁.
I, б. Проектируем остальные боковые ребра - отрезки, равные и параллельные первому ребру СЕ.
I, в. Проектируем верхнее основание призмы как многоугольник, равный и параллельный нижнему основанию, получаем комплексный чертеж призмы.
Выявляем на проекциях невидимые элементы. Фронтальную проекцию ребра ВМ и горизонтальную проекцию стороны основания CD изображаем штриховыми линиями как невидимые.
I, г. Дана фронтальная проекция Q₂ точки Q на проекции A₂K₂F₂D₂ боковой грани; требуется найти ее горизонтальную проекцию. Для этого проводим через точку Q₂ в проекции A₂K₂F₂D₂ грани призмы вспомогательную прямую, параллельную боковым ребрам этой грани. Находим горизонтальную проекцию вспомогательной прямой и на ней при помощи вертикальной линии связи определяем место искомой горизонтальной проекции Q₁ точки Q.
II. Развертка поверхности призмы.
Имея на горизонтальной проекции натуральные размеры сторон основания, а на фронтальной - размеры ребер, можно построить полную развертку поверхности данной призмы.
Будем катить призму, повертывая ее каждый раз вокруг бокового ребра, тогда каждая боковая грань призмы на плоскости будет оставлять след (параллелограмм), равный ее натуральной величине. Построение боковой развертки будем производить в следующем порядке:
а) из точек А₂, В₂, D₂ . . . Е₂ (фронтальных проекций вершин оснований) проводим вспомогательные прямые, перпендикулярные к проекциям ребер;
б) радиусом R (равным стороне основания CD) делаем на вспомогательной прямой, проведенной из точки D₂, засечку в точке D; соединив прямой точки С₂ и D и проведя прямые, параллельные E₂С₂ и C₂D, получим боковую грань CEFD;
в) затем, аналогично пристроив следующие боковые грани, получим развертку боковых граней призмы. Для получения полной развертки поверхности данной призмы пристраиваем к соответствующим граням основания.
III. Наглядное изображение призмы в изометрии.
III, а. Изображаем нижнее основание призмы и ребро СЕ, пользуясь координатами согласно (фиг.284 I, a).
III, б. Изображаем боковые ребра и верхнее основание. Определив невидимые ребра и стороны основания, обводим их штриховыми линиями.

Пирамида.....