Пересечение прямой с плоскостью.
Если прямая не лежит в плоскости и не параллельна ей, она пересекает плоскость.
Задача на определение точки пересечения прямой с плоскостью сводится к следующему:
1) проведению вспомогательной плоскости (Вспомогательную плоскость рекомендуется выбирать такую, которая даст наиболее простое графическое решение задачи) через данную прямую;
2) нахождению линии пересечения вспомогательной плоскости с данной плоскостью;
3) определению точки пересечения данной прямой с линией пересечения плоскостей, а следовательно, с данной плоскостью.
Пересечение прямой с проектирующей плоскостью.
Пример 1. На (фиг.250,а) даны плоскость δ (δ1) и прямая АВ (А1В1 и А2В2); требуется определить точку их пересечения.
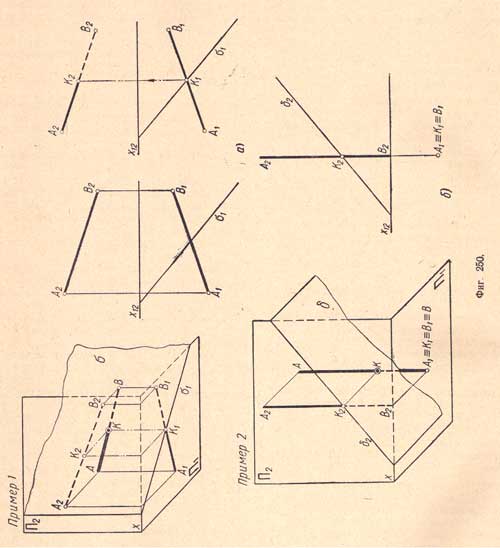
В этом случае нет надобности прибегать к вспомогательной плоскости, так как данная плоскость δ - горизонтально - проектирующая. По свойству проектирующих плоскостей горизонтальная проекция точки пересечения, лежащая в плоскости δ, сливается с горизонтальной проекцией δ1.
Поэтому точка К1 пересечения горизонтальной проекции А1В1 прямой АВ с горизонтальной проекцией δ1 есть горизонтальная проекция точки пересечения К; фронтальная проекция К2 определяется путем проведения вертикальной линии связи до пересечения ее с фронтальной проекцией А2В2.
Пример 2. На (фиг.250,б) приведен пример пересечения прямой АВ с фронтально - проектирующей плоскостью δ.
Пересечение прямой с плоскостью общего положения.
Пример 1. Даны: плоскость общего положения а и прямая общего положения АВ (А1В1 А2В2); требуется найти точку их пересечения (фиг.251,а).
Проводим через прямую АВ какую - либо вспомогательную плоскость, например горизонтально - проектирующую плоскость δ (δ1), как показано на (фиг.251,б); она пересечет плоскость a по прямой NM (N1M1, N2М2), которая, в свою очередь, пересечет прямую АВ (А1В1 А2В2) в точке С (С1С2), что видно на (фиг.251,в). Точка С есть точка пересечения прямой АВ с плоскостью а.
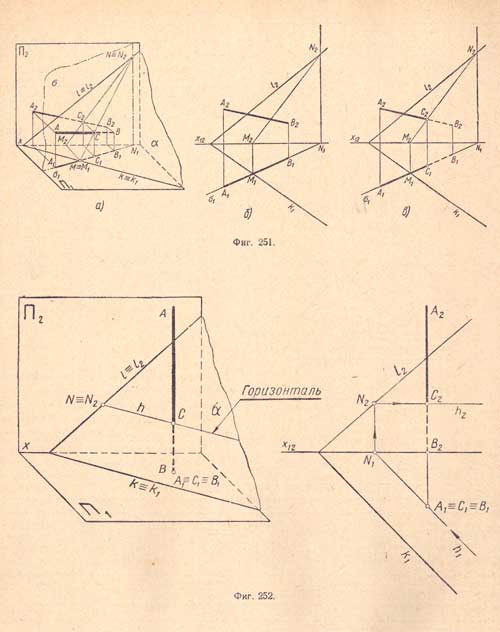
Пример 2. На (фиг.252) приведен пример нахождения проекций точки пересечения прямой AB c плоскостью общего положения при помощи горизонтали h.
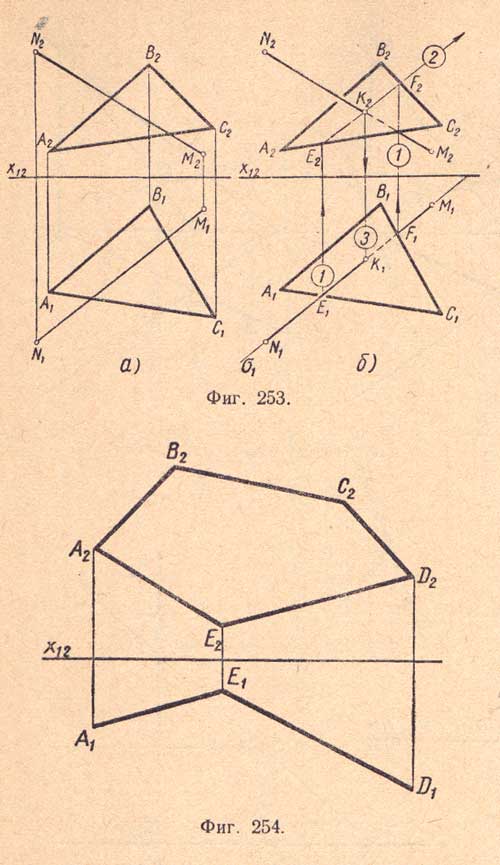
Пример 3. Даны: треугольник ABC и прямая NM; требуется определить точку их пересечения (фиг.253,а).
Возьмем в качестве вспомогательной плоскости горизонтально - проектирующую плоскость δ, тогда горизонтальная проекция ог сольется с горизонтальной проекцией N1M1 прямой NM и пересечет проекции сторон треугольника в точках Е1 и F1 (фиг.253,б). Отрезок Е1F1 будет горизонтальной проекцией линии пересечения. Затем находим фронтальную проекцию линии пересечения: при помощи вертикальных линий связи получаем точки Е2 и F2, проводим через них прямую E2F2, которая будет фронтальной проекцией линии пересечения.
Прямая E2F2 пересекает прямую N2М2 в точке К2. Точка К2 будет фронтальной проекцией точки пересечения прямой MN с прямой EF; горизонтальную проекцию K1 этой точки определяем при помощи вертикальной линии связи.
Точка К (K1, К2) будет точкой пересечения данной прямой MN с данным треугольником ABC, как одновременно им принадлежащая, потому что прямая MN пересекается в ней с прямой EF, лежащей в плоскости треугольника ABC.
Упражнение 1
Построить комплексный чертеж треугольника ABC по данным координатам вершин. Найти натуральную величину сторон треугольника и построить его в натуральную величину. По этим же координатам построить наглядное изображение
Упражнение 2
По данным фронтальной проекции многоугольника и горизонтальным проекциям двух смежных сторон его достроить горизонтальную проекцию многоугольника.
В плоскости многоугольника построить проекции произвольного треугольника. Построить точку вне многоугольника, но лежащую в одной плоскости с ним (фиг.254)
Читай также: Условия видимости.....











