Пересечение многогранников и тел вращения.
Пересечение поверхностей многогранников с поверхностями тел вращения.
А) Построение линии пересечения поверхностей прямой четырехугольной призмы и прямого кругового цилиндра (фиг.352)
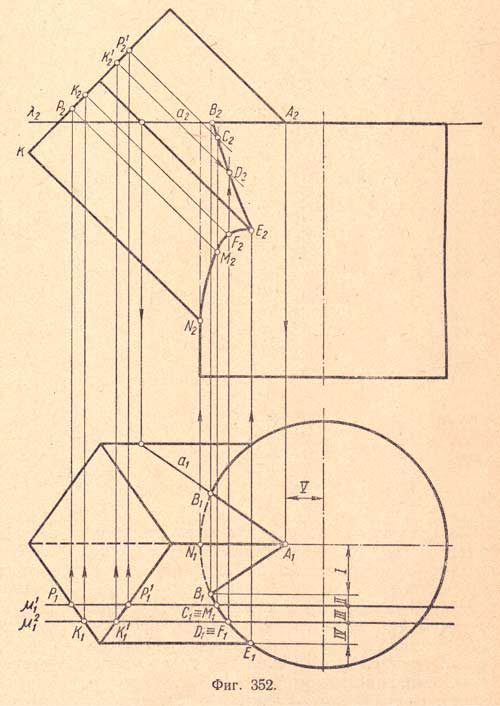
1. Ось вращения цилиндра перпендикулярна плоскости П1; боковые ребра призмы параллельны плоскости П2 и наклонны к плоскости П1.
Горизонтальные проекции А1, Е1 и N1 и фронтальные проекции А2, Е2 и N2 точек пересечения ребер призмы с основанием и с боковой поверхностью цилиндра определяются без дополнительных построений.
Для определения проекций точек линии пересечения боковых граней призмы с боковой поверхностью цилиндра применяем фронтальные секущие плоскости μ1 и μ2. Эти плоскости рассекают боковую поверхность цилиндра и боковые грани призмы по прямым, пересечения которых дадут общие точки, принадлежащие как боковой поверхности цилиндра, так и боковым граням призмы, т.е. точки, принадлежащие искомой линии пересечения.
Например, при сечении плоскостью μ2 получим точки D и F (D1, F1 и D2, F2) и т.д.
Для определения линии пересечения верхнего основания цилиндра с боковыми гранями призмы вводим горизонтальную секущую плоскость λ, проходящую по верхнему основанию цилиндра. Эта плоскость пересекает грань призмы по прямой а, горизонтальная проекция которой пересекает окружность - проекцию верхнего основания цилиндра - в точке В1. Соединив точку В1 с точкой A1 прямой, получим горизонтальную проекцию линии пересечения грани призмы с основанием цилиндра.
Ее фронтальная проекция сливается с фронтальной проекцией верхнего основания цилиндра.
Найденные фронтальные проекции стальных точек соединяем плавными кривыми и получаем фронтальную проекцию видимой части линии пересечения.
Проекция невидимой части симметрична видимой и сливается с ней.
2. Для построения аксонометрической (изометрической) проекции пересекающихся поверхностей цилиндра с призмой сначала строят изометрические проекции цилиндра и основания призмы (фиг.353,а).
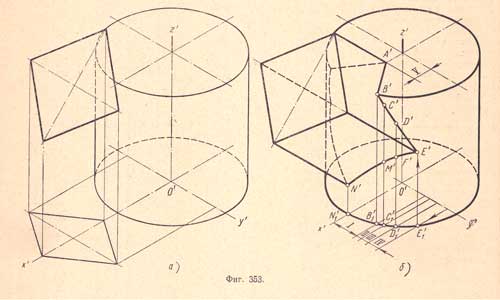
Потом на нижнем основании цилиндра отмечают точки N'1, В'1, C'1, D'1 и Е'1 - вторичные проекции линии пересечения, для чего используют размеры I, II, III и IV. После этого из полученных точек проводят прямые параллельно оси z' и на них откладывают высоты этих точек. Найденные точки В', С", D', Е', F', М' и N' последовательно соединяют двумя плавными кривыми. Пользуясь размером V, определяют точку А' - пересечение ребра призмы с верхним основанием цилиндра - и соединяют ее с точкой В', получают видимую часть линии пересечения. Затем находят невидимую часть линии пересечения и проводят боковые ребра призмы; получают изометрическую проекцию пересекающихся цилиндра с призмой (фиг.353,б).
Б) Построение линии пересечения поверхностей правильной шестиугольной призмы и прямого кругового конуса (фиг.354)
1. Ось вращения конуса перпендикулярна плоскости Пг и проходит через центры оснований призмы.
В данном случае достаточно найти проекции точек А и В, так как остальные подобные им точки определяются без дополнительных построений (фиг.354,а).
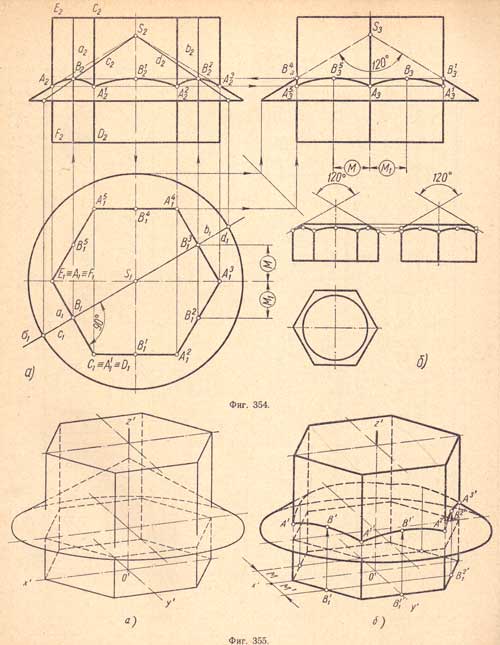
Горизонтальная и фронтальная проекции точки А (A1, A2) пересечения бокового ребра призмы с поверхностью конуса определяются без построений.
Горизонтальная проекция В1 промежуточной точки В определяется пересечением проекции Е1С1 стороны основания призмы с горизонтальной проекцией δ1, введенной вспомогательной горизонтально - проектирующей плоскости δ, расположенной под углом 90° к стороне ЕС основания призмы. Фронтальная проекция В2 этой точки определяется точкой пересечения проекции с2 образующей конуса с проекцией прямой а2, полученных в результате сечения поверхностей конуса и призмы плоскостью δ.
Профильные проекции всех точек находятся, как третьи проекции, по двум данным.
Последовательно соединив фронтальные, а также профильные проекции найденных точек кривыми, получим фронтальные и профильные проекции линий пересечения (гиперболы) поверхности конуса с боковыми гранями призмы. Горизонтальные проекции этих кривых сольются с проекцией основания призмы.
Такое построение применяется при изображении фасок гайки, когда она вычерчивается по действительным размерам (фиг.354,б).
2. Для построения дяметрической проекции пересекающихся поверхностей конуса с призмой сначала строят диметрическую проекцию призмы и конуса (фиг.355,а).
Потом определяют вторичные проекции промежуточных точек В, из которых проводят вспомогательные прямые параллельно ребрам призмы. На этих прямых определяют диметрические проекции промежуточных точек, а на боковых ребрах призмы - диметр ические проекции точки А, пользуясь в обоих случаях аппликатами этих точек.
Затем полученные точки последовательно соединяют кривыми линиями; получают диметрическую проекцию линии пересечения. Проведя контурные образующие конуса, заканчивают построение диметрической проекции пересекающихся конуса с призмой (фиг.355,б).
Аксонометрические проекции деталей.....











