Пирамида.
Пирамидой называется многогранник, у которого одна из граней - основание - какой - нибудь многоугольник, а все остальные - боковые - треугольники, имеющие общую вершину.
Общая вершина S боковых граней называется вершиной пирамиды, а перпендикуляр SO, опущенный из вершины на плоскость основания, - высотой ее (фиг.286,а).
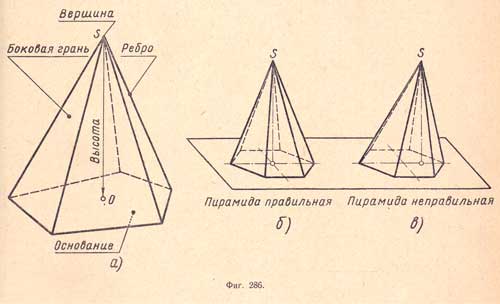
Пирамиды бывают: треугольные, четырехугольные и т. д., смотря по тому, что является основанием - треугольник, четырехугольник и т. д.
Пирамида называется правильной (фиг.286,б), если, во - первых, ее основанием является правильный многоугольник, и, во - вторых, высота проходит через центр этого многоугольника.
В противном случае пирамида называется неправильной (фиг.286,в). В правильной пирамиде все боковые ребра равны между собой (как наклонные с равными проекциями). Поэтому все боковые грани правильной пирамиды есть равные равнобедренные треугольники.
Анализ элементов правильной шестиугольной пирамиды и их изображение на комплексном чертеже (фиг.287).
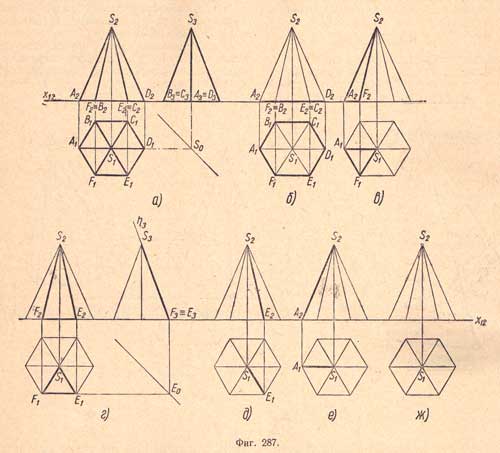
а) Комплексный чертеж правильной шестиугольной пирамиды. Основание пирамиды расположено на плоскости П1; две стороны основания пирамиды параллельны плоскости проекций П2.
б) Основание ABCDEF - шестиугольник, расположенный в плоскости проекций П1.
в) Боковая грань ASF - треугольник, расположенный в плоскости общего положения.
г) Боковая грань FSE - треугольник, расположенный в профильно - проектирующей плоскости .
д) Ребро SE - отрезок общего положения.
е) Ребро SA - фронтальный отрезок.
ж) Вершина S пирамиды - точка в пространстве.
На (фиг.288 и фиг.289) приведены примеры последовательных графических операций при выполнении комплексного чертежа и наглядных изображений (аксонометрии) пирамид.
Изображение правильной пятиугольной пирамиды.
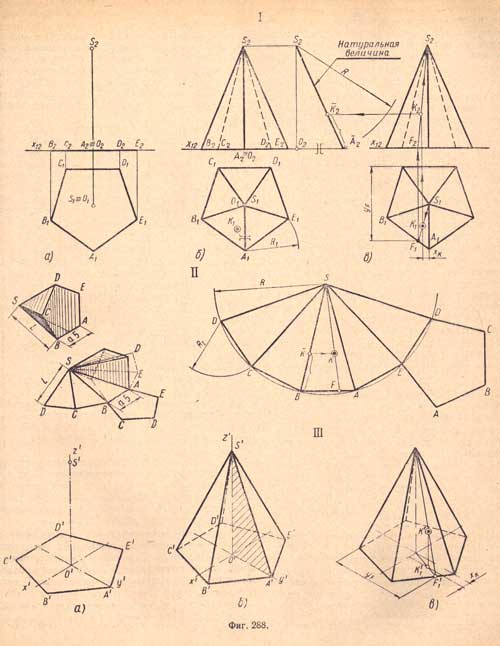
Дано:
1. Основание расположено на плоскости П1.
2. Одна из сторон основания параллельна оси х12.
I. Комплексный чертеж.
I, а. Проектируем основание пирамиды - многоугольник, по данному условию лежащий в плоскости П1.
Проектируем вершину - точку, расположенную в пространстве. Высота точки S равна высоте пирамиды. Горизонтальная проекция S1 точки S будет в центре проекции основания пирамиды (по условию).
I, б. Проектируем ребра пирамиды - отрезки; для этого соединяем прямыми проекции вершин основания ABCDE с соответствующими проекциями вершины пирамиды S. Фронтальные проекции S2 С2 и S2 D2 ребер пирамиды изображаем штриховыми линиями, как невидимые, закрытые гранями пирамиды (SBА и SAE).
I, в. Дана горизонтальная проекция К1 точки К на боковой грани SBА, требуется найти ее фронтальную проекцию. Для этого проводим через точки S1 и K1 вспомогательную прямую S1F1, находим ее фронтальную проекцию и на ней при помощи вертикальной линии связи определяем место искомой фронтальной проекции K2 точки К.
II. Развертка поверхности пирамиды - плоская фигура, состоящая из боковых граней - одинаковых равнобедренных треугольников одна сторона которых равна стороне основания, а две другие - боковым ребрам, и из правильного многоугольника - основания.
Натуральные размеры сторон основания выявлены на его горизонтальной проекции. Натуральные размеры ребер на проекциях не выявлены.
Гипотенуза S2¯A2 (фиг.288, 1, б) прямоугольного треугольника S2O2¯A2, у которого большой катет равен высоте S2O2 пирамиды, а малый - горизонтальной проекции ребра S1A1 является натуральной величиной ребра пирамиды. Построение развертки следует выполнять в следующем порядке:
а) из произвольной точки S (вершины) проводим дугу радиусом R, равным ребру пирамиды;
б) на проведенной дуге отложим пять хорд размером R1 равным стороне основания;
в) соединим прямыми точки D, С, В, А, Е, D последовательно между собой и с точкой S, получим пять равнобедренных равных треугольников, составляющих развертку боковой поверхности данной пирамиды, разрезанной по ребру SD;
г) пристраиваем к любой грани основание пирамиды - пятиугольник, пользуясь способом триангуляции, например к грани DSE.
Перенос на развертку точки К осуществляется вспомогательной прямой с помощью размера В1F1, взятого на горизонтальной проекции, и размера А2К2, взятого на натуральной величине ребра.
III. Наглядное изображение пирамиды в изометрии.
III, а. Изображаем основание пирамиды, пользуясь координатами согласно (фиг.288, 1, а).
Изображаем вершину пирамиды, пользуясь координатами по (фиг.288, 1, а).
III, б. Изображаем боковые ребра пирамиды, соединяя вершину с вершинами основания. Ребро S'D' и стороны основания C'D' и D'E' изображаем штриховыми линиями, как невидимые, закрытые гранями пирамиды C'S'B', B'S'A' и A'S'E'.
III, e. Определяем на поверхности пирамиды точку К, пользуясь размерами уF и хK. Для ди-метрического изображения пирамиды следует придерживаться той же последовательности.
Изображение неправильной треугольной пирамиды.
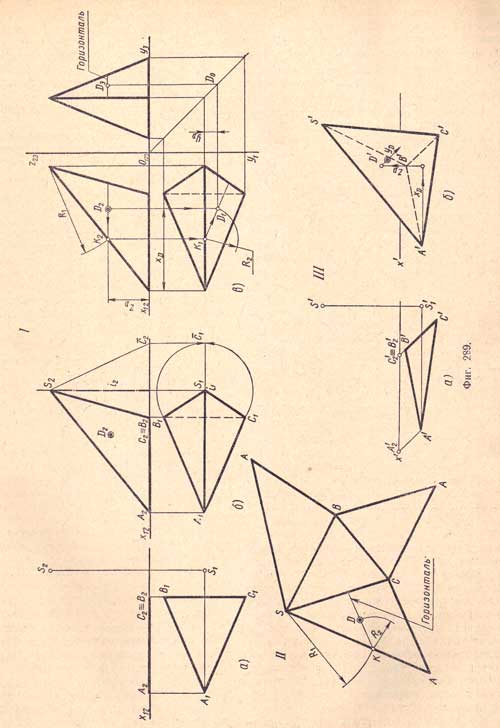
Дано:
1. Основание расположено на плоскости П1.
2. Сторона ВС основания перпендикулярна оси X.
I. Комплексный чертеж
I, а. Проектируем основание пирамиды - равнобедренный треугольник, лежащий в плоскости П1, и вершину S - точку, расположенную в пространстве, высота которой равна высоте пирамиды.
I, б. Проектируем ребра пирамиды - отрезки, для чего соединяем прямыми одноименные проекции вершин основания с одноименными проекциями вершины пирамиды. Горизонтальную проекцию стороны основания ВС изображаем штриховой линией, как невидимую, закрытую двумя гранями пирамиды ABS, ACS.
I, в. На фронтальной проекции A2С2S2 боковой грани дана проекция D2 точки D. Требуется найти ее горизонтальную проекцию. Для этого через точку D2 проводим вспомогательную прямую параллельно оси х12 - фронтальную проекцию горизонтали, затем находим ее горизонтальную проекцию и на ней, при помощи вертикальной линии связи, определяем место искомой горизонтальной проекции D1 точки D.
II. Построение развертки пирамиды.
Натуральные размеры сторон основания выявлены на горизонтальной проекции. Натуральная величина ребра AS выявлена на фронтальной проекции; натуральной величины ребер BS и CS в проекциях нет, величину этих ребер выявляем путем вращения их вокруг оси i, перпендикулярной к плоскости П1 проходящей через вершину пирамиды S. Новая фронтальная проекция ¯C2S2 является натуральной величиной ребра CS.
Последовательность построения развертки поверхности пирамиды:
а) вычерчиваем равнобедренный треугольник - грань CSB, основание которого равно стороне основания пирамиды СВ, а боковые стороны - натуральной величине ребра SC;
б) к сторонам SC и SB построенного треугольника пристраиваем два треугольника - грани пирамиды CSA и BSA, а к основанию СВ построенного треугольника - основание СВА пирамиды, в результате получаем полную развертку поверхности данной пирамиды.
Перенос на развертку точки D выполняется в следующем порядке: сначала на развертке боковой грани ASC проводим линию горизонтали при помощи размера R1 а затем определяем на линии горизонтали место точки D при помощи размера R2.
III. Наглядное изображение пирамиды е фронтальной диметрической проекции
III, а. Изображаем основание А'В'С и вершину S' пирамиды, пользуясь координатами согласно (фиг.289, 1, а).
III, б. Изображаем ребра S'A, S'C' и S'B' пирамиды, соединяя вершину S' с вершинами основания А'В'С'. Ребро S'B' и стороны основания A'В' и В'С' изображаем штриховыми линиями, как невидимые, закрытые гранью A'S'C'. Для определения на поверхности пирамиды места точки D пользуемся координатами точки xD, yD, zD (фиг.289, 1, в), причем координата yD сокращается вдвое.
Вращения и развертки поверхностей.....











