Окружность, дуги и многоугольники.
Проведение дуги или окружности через три заданные точки. Через три данные точки А, В и С, не лежащие на одной прямой, можно провести только одну окружность (или дугу); причем ее центр О определяют следующим построением: соединив
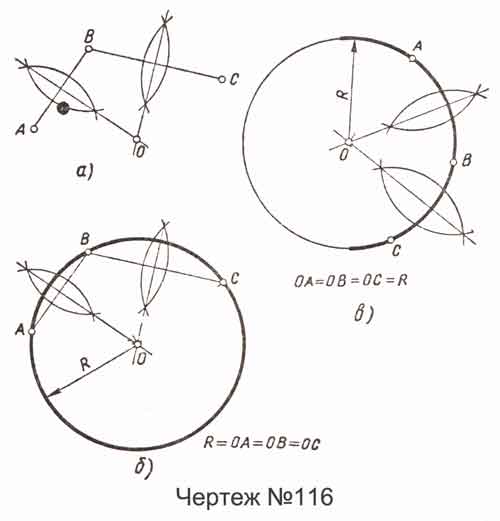
отрезками точки А и В, а также точки В и С, делят эти отрезки пополам; точка О пересечения линий деления явится центром искомой окружности (чертеж-№116, а). Из центра Сопроводят искомую окружность (или дугу) радиусом R = ОА = ОВ = ОС (чертеж-№116, б).
Нахождение центра О и величины радиуса R данной окружности (или дуги).
Решение этой задачи вытекает из предыдущего построения: на данной дуге намечают три точки А, В и С. Дуги АВ и ВС делят пополам. Точка О пересечения линий деления является искомым центром, а отрезок ОА = ОВ = ОС является радиусом R данной дуги (чертеж-№116, в).
Деление окружности на равные части и вписывание правильных многоугольников.
На чертеже-№117 показаны построения, применяемые при делении окружности на 4, 8, 3, 6, 12 и 5 равных частей и изображения правильных вписанных многоугольников с соответствующим числом сторон.
Деление окружности на 4 равные части.
Точки А, В, С и D пересечения взаимно перпендикулярных диаметров (центровых линий) с окружностью явятся точками деления окружности на 4 равные части. Соединив последовательно эти точки, получим квадрат, стороны которого будут наклонены на угол 45°.
Для изображения вписанного квадрата со сторонами, расположенными параллельно центровым линиям, дуги АВ и ВС делят пополам; линии деления продолжают до пересечения с дугами CD и AD. Остальное выполнение видно из чертежа.
Построение вписанного правильного восьмиугольника аналогично предыдущему (чертеж-№117,а).
Деление окружности на 3 и 6 равных частей.
Для деления окружности на 3 равные части засечки на окружности получают при проведении дуги радиусом R, приняв за центр любую точку на окружности, например точку D; для деления окружности на шесть равных частей проводят две дуги радиусом R, приняв за центры концы одного и того же диаметра, например точки В и D. Остальное выполнение понятно из чертежа (чертеж-№117, б).
Деление окружности на 12 равных частей.
Искомые точки на окружности получают путем проведения четырех дуг радиусом R; центрами этих дуг являются концы двух взаимно - перпендикулярных диаметров (чертеж-№117, в).
Деление окружности на 5 равных частей.
Половину диаметра, например отрезок ОМ, делят пополам; из полученной точки Р, как из центра, проводят дугу радиусом R1 = PL ; она пересекает отрезок ОК в точке Q. Отрезок LQ равен искомой стороне правильного вписанного пятиугольника. Из центра L радиусом R2 = LQ засекают на окружности точки А и В. Приняв за центры точки А и В, тем же радиусом R2 засекают на окружности точки D и С. Остальное выполнение понятно из чертежа (чертеж-№117, г).
На (чертеже-№117, д) показан пример применения деления окружности при выполнении контура технической детали.
Деление окружности на произвольное число равных частей
Деление окружности на произвольное число равных частей можно выполнить, пользуясь коэффициентами, приведенными в таблице-№5.
Для определения величины хорды, стягивающей требуемую часть окружности (а следовательно, длину стороны соответствующего правильного вписанного многоугольника), надо диаметр окружности умножить на коэффициент. Например, окружность D = 41 разделить на 9 частей; для этого 41 X 0,34202 = 14,02282 ≈ 14,
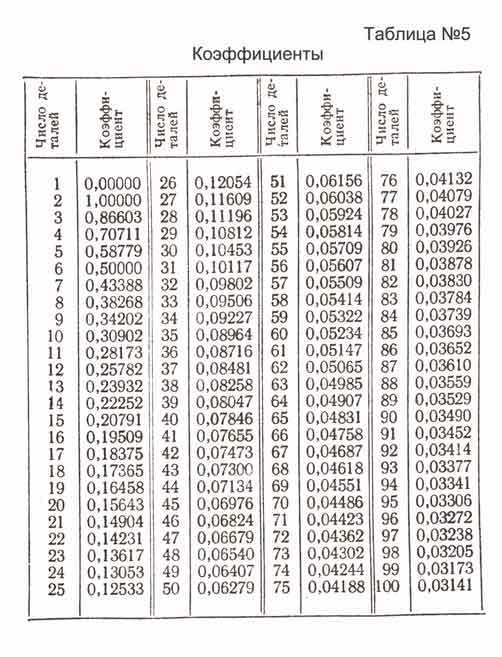
т. е. длина хорды, стягивающей 1/9 часть окружности, приблизительно равна 14 мм. Дальнейшее построение делаем аналогично указанным ранее. Недостатком такого деления является некоторая неточность, получающаяся из - за невозможности точно отмерить на бумаге длину радиуса, выраженную количеством миллиметров с десятыми или даже сотыми долями.
УПРАЖНЕНИЕ 5
Пример 1. Для закрепления темы «Деление окружности» следует выполнить контур изображенной на чертеже-№117, е детали по одному из шести данных вариантов.
Пример 2. Перечертить один из вариантов контуров, изображенных на чертеже-№117, ж.
Построение правильных многоугольников по заданной стороне
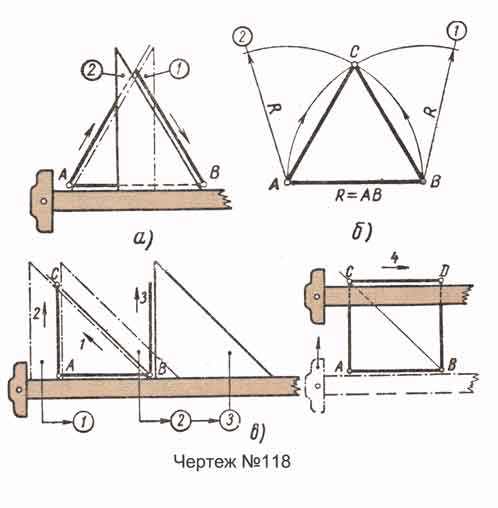
Треугольник. На чертеже-№118, а показано построение правильного треугольника по данной стороне А В, выполненное при помощи рейсшины и угольника 30° - 60° - 90°, а на чертеже-№118, б - при помощи циркуля и рейсшины; последовательность построения видна из чертежа и не требует пояснений.
Квадрат. На чертеже-№118, в показано построение квадрата по данной стороне АВ, выполненное при помощи рейсшины (линейки) и угольника 45° - 45° - 90°; построение начинают с проведения из точки В наклонной прямой подуглом 45°; порядок остального построения показан цифрами и не требует пояснений.
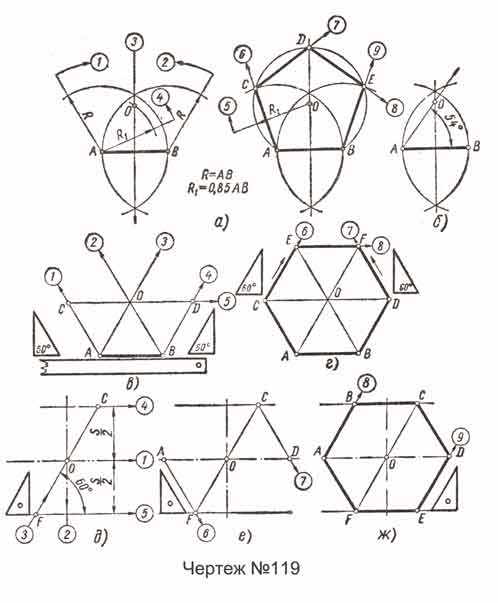
Пятиугольник. На чертеже-№119, а показано построение правильного пятиугольника по данной стороне АВ, выполненное при помощи циркуля и рейсшины (линейки). Последовательность построения показана цифрами и не требует дополнительных пояснений. Радиус R1 окружности, описанной около пятиугольника, равен 0,85 АВ. Вычисление рекомендуем проводить в такой последовательности: определить 0,1 от АВ, определить половину этой величины и сложить их и полученную сумму вычесть из АВ; например, при АВ = 30 R1 = 30 - (3 + 1,5) = 25,5.
Центр О можно найти и другими способами, например проведением из точки А луча под углом 54° при помощи транспортира (чертеж-№119, б).
Шестиугольник. На чертеже-№119, в и г показано построение правильного шестиугольника по данной стороне АВ, выполненное при помощи угольника 30° - 60° - 90° и рейсшины; а на чертеже-№119, д - ж - построение той же фигуры, выполненное по данному размеру s (под ключ). Последовательность построения везде показана цифрами в кружках.
Построение правильного многоугольника (с любым числом сторон) по данной стороне а.
Для того чтобы построить правильный многоугольник по данной стороне а, предварительно вычисляют радиус R1 описанной окружности, пользуясь коэффициентами, приведенными в таблице-№6.
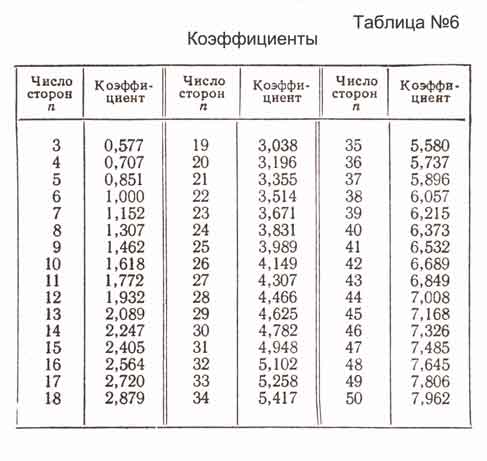
Радиус R1 равен коэффициенту, умноженному на длину данной стороны.
Пример. Построить правильный семиугольник, у которого сторона АВ = 20 (чертеж-№120).
Пользуясь таблицей, вычисляют значение R1 для n = 7: 20 X 1,152 = 23,04.
Последовательность построения показана на чертеже-№120 цифрами в кружках.
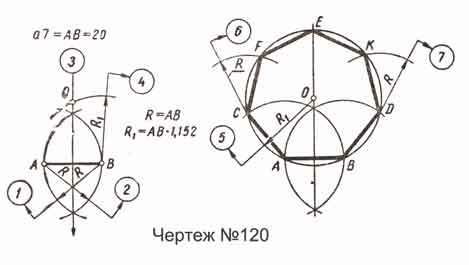
Построение треугольника по трем заданным сторонам.
Даны стороны а = 30; b = 45; с = 60 заданного треугольника (чертеж-№121, а).
За основу построения можно принять любую сторону; в данном случае принята сторона с = АС = 60. Порядок построения показан цифрами (чертеж-№121, б).
Построение равных многоугольников.
Координатный метод. Координатами какой-либо точки, лежащей на плоскости, называются расстояния от этой точки до любых двух взаимно перпендикулярных прямых, лежащих в той же плоскости, называемых осями координат; из них горизонтальная ось Ох называется осью абсцисс, а вертикальная Оy - осью ординат; точка О пересечения осей называется началом координат (чертеж-№122, а).
Абсциссой точки А является отрезок ААY, который измеряют равным ему отрезком ОАХ по оси абсцисс ОX; ординатой точки А является отрезок ААХ, который измеряется равным ему отрезком OАY по оси ординат ОY.
Следовательно, место точки А (чертеж-№122, б) можно найти путем откладывания по оси ОX от начала координат (отточки О) отрезка ОАХ, равного подразумеваемой абсциссе ААУ, а затем откладывания ординаты ААХ на перпендикуляре, проведенном из точки АХ к оси ОХ.
Пример. Построить многоугольник A1 B1 C1 D1, равный данному ABCD (чертеж-№123).
а) Из каждой вершины данного многоугольника ABCD опускаем перпендикуляры на ось абсцисс (Ох) - получим точки АX, ВX, СX, DX (чертеж-№123, а).
б) На заранее выбранном для построения равного многоугольника месте проводим ось абсцисс и намечаем на ней точки AX1, BX1, СX1, DX1, одинаково расположенные с точками АX, ВX, СX, и DX, т. е. откладываем абсциссы точек A, В, С и D. Из этих точек проводим перпендикуляры (линии, параллельные оси ординат) на высоту, соответствующую высоте аналогичных точек данного многоугольника, т. е. на каждом перпендикуляре откладываем ординату соответствующей точки. Получим точки А1 В1 С1 и D1 (чертеж-№123, б).
в) Последовательно соединив точки А1 и В1; В1 и С1 и т. д. отрезками прямых, получим многоугольник A1B1C1D1, равный данному (чертеж-№123, в).
За ось ОX или ОY можно принять одну из сторон данной фигуры, например AD (чертеж-№123, г), и построить равную фигуру, наклонив на любой угол в произвольном направлении новую ось абсцисс, совпадающую с намеченной стороной AD фигуры. Построения, показанные на чертеж-№123, г-е, аналогичны показанным на чертеж-№123, а-в.
Метод триангуляции. Этот метод основан на разбивке данного многоугольника на треугольники и последовательного построения треугольников по данным сторонам. Разберем такой же, как и в первом случае,пример:
а) разбиваем данный многоугольник ABCD на два треугольника ABD и BCD (чертеж-№124, а);
б) приняв за основание сторону AD, проводим отрезок A1D1 = AD и строим треугольник A1B1D1 равный треугольнику ABD (чертеж-№121) по трем данным сторонам (чертеж-№124, б);
в) приняв за основание сторону B1D1 строим треугольник B1C1D1 равный треугольнику BCD (чертеж-№124, в).
УПРАЖНЕНИЕ 6
Пример 1 (чертеж-№125, а). Построить пятиугольник, равный данному, методом координирования (в том же положении, в каком он показан на фигуре).
Пример 2 (чертеж-№125, б). Построить четырехугольник, равный данному, методом триангуляции, расположив его так, чтобы сторона ВС была горизонтальна.
Чертежи используемые в данной главе: >>> Чертеж №117 >>> Чертеж №122 №123 >>> Чертеж №124 №125 >>> Смотри также >>> Сопряжения.....











