Пересечение конуса и шара.

Пересечение поверхностей усеченного кругового конуса и шара (фиг.344)

I. Ось шара и ось вращения конуса перпендикулярны плоскости П₁.
Фронтальные проекции характерных точек А и В определяются пересечением фронтальных проекций контурных образующих конуса с проекцией главного меридиана поверхности шара.
Фронтальные и горизонтальные проекции характерных точек определяются при помощи введения вспомогательной профильной плоскости θ. Эта плоскость рассекает сферу по окружности (радиус R), проекция которой, пересекаясь с профильными проекциями контурных образующих конуса, дает точки С₃ и D₃ - профильные проекции характерных точек.
По этим профильным проекциям точек находят их горизонтальные и фронтальные проекции С₁ и D₁ С₂ и D₂ (фиг.344,а).

Проекции промежуточных точек Е, F, М, К, Р и Q определяются при помощи ряда вспомогательных горизонтальных плоскостей λ¹, λ², λ³. Эти плоскости пересекут каждое тело по соответствующей окружности — параллели, которые, пересекаясь между собой, определяют точки, одновременно принадлежащие поверхности шара и поверхности конуса, а следовательно, и линии пересечения.
Горизонтальные проекции параллелей конуса проведены из точки O¹₁, а шара из точки O₁.
Пересечения этих параллелей определяют горизонтальные проекции Е₁, F₁, М₁, Q₁, Р₁ и К₁ точек линии пересечения. Фронтальные проекции Е₁, F₁, М₁, Q₁, Р₁ и К₁ этих точек, найденные при помощи вертикальных линий связи, лежат на проекциях λ¹₂, λ²₂, λ³₂.
Найденные как горизонтальные, так и фронтальные проекции всех точек соединяют плавными кривыми и получают искомые проекции линии пересечения (фиг.344,б).
Для построения аксонометрической проекции (изометрии) пересекающихся поверхностей конуса с шаром (фиг.345)

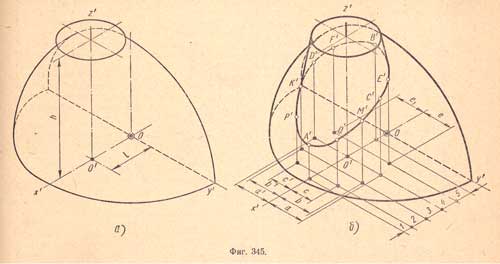
сначала строят изометрическую проекцию четверти шара и верхнее основание конуса (фиг.345,а). Потом строят горизонтальную вторичную проекцию точек линии пересечения (по ординатам и абсциссам). Из полученных проекций точек проводят прямые, параллельные оси z', на которых откладывают высоты (аппликаты точек линии перехода), взяв их с фронтальной проекции; после этого соединяют найденные точки плавной кривой и получают изометрическую проекцию линии пересечения (фиг.345,6).

II. Построение линий пересечения поверхностей вращения при помощи концентрических сфер.
При пересечении поверхности шара с поверхностью тела вращения, ось которого проходит через центр сферы, получается окружность. На (фиг.346) показано пересечение шара с прямым круговым цилиндром и прямым круговым конусом.

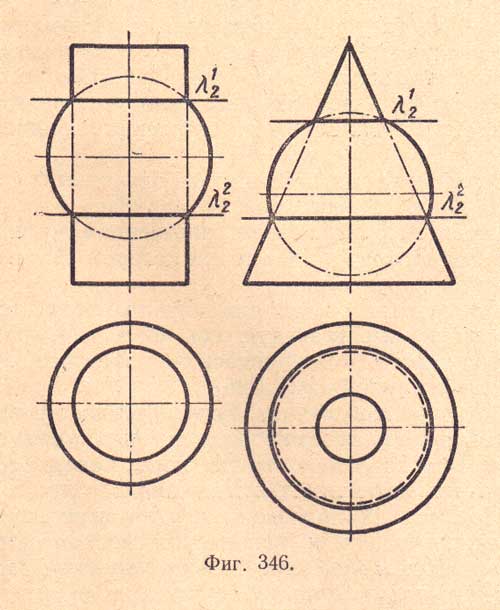
Показанные цилиндр и шар, а также конус и шар имеют общие оси вращения, поэтому данные тела называются соосными.
Эти соосные тела пересекаются по окружностям, лежащим в плоскостях, перпендикулярных к их общей оси вращения.
Оси вращения цилиндра и конуса перпендикулярны плоскости П₁. Горизонтальные проек-: ции линий пересечения выявлены окружной стями, а фронтальные - отрезками, равными натуральной величине диаметров.
Приведенные примеры являются основой спо-' соба построения линии пересечения поверхностей двух тел вращения при помощи концентрических сфер.
Разберем несколько примеров:

А) Пересечение поверхностей двух цилиндров разных диаметров, данных одной проекцией.

Б) Пересечение поверхностей вращения: а) конуса с конусом; б) цилиндра с конусом: в) тора с тором.