Аксонометрическая проекция окружности.
ПОСТРОЕНИЕ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ ОКРУЖНОСТИ.
1. Построение изометрической проекции окружности, лежащей в одной из плоскостей проекции.
I, а. Дана окружность диаметра D, лежащая в плоскости П1 (фиг.278). Намечаем на ней несколько равномерно расположенных (но не менее восьми) точек, проекции которых на плоскости П1 обозначим А1,В1,С1,D1,Е1,F1,G1,H1. Определяем их координаты.
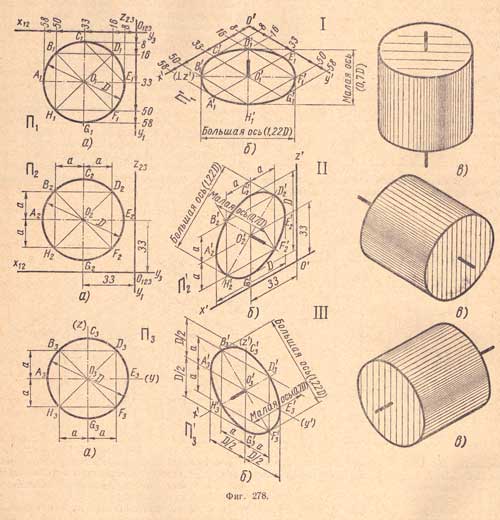
I, б. Проводим аксонометрические оси х' и у' и строим на плоскости Щ вторичные изометрические проекции всех указанных точек. Соединив их плавной замкнутой кривой, получим вторичную и вместе с тем изометрическую проекцию данной окружности - эллипс, у которого малая ось будет иметь направление не лежащей в данной плоскости изометрической оси г (т. е. вертикальной) и равняться 0,7 D, а большая ось будет перпендикулярна малой оси (т. е. иметь горизонтальное направление) и равняться 1,22 D.
I, в. Показан пример применения изометрической проекции круга, лежащего в горизонтальной плоскости, при изображении изометрической проекции цилиндра.
II, а. Дана ортогональная проекция той же окружности, но лежащей в плоскости П2. Вместо того, чтобы определять координаты всех намеченных точек, можно определять только координаты центра О2 и размеры а и а от центровых линий до намеченных точек В2,D2,H2,F2.
II, б. Построение вторичной и вместе с тем изометрической проекции этой окружности аналогично указанному на (фиг.278, I, б). Малая ось полученного эллипса расположена по направлению не лежащей в д'анной плоскости аксонометрической оси у', а большая ось перпендикулярна ей.
Длина осей эллипса такая же, как и на (фиг.278, I, б).
II, в. Показан пример применения изометрической проекции окружности, лежащей во фронтальной плоскости при изображении цилиндра.
III, а. Дана ортогональная проекция той же окружности, но лежащей в плоскости П3; центр окружности не координирован. Определяем размеры а и а от центровых линий до намеченных точек В3, D3, F3 и Н3.
III, б. Построение эллипса начинаем с проведения прямых, заменяющих аксонометрические оси z и у, затем через полученную в пересечении точку O3 проводим линию малой оси по направлению не лежащей в данной плоскости аксонометрической оси х и линию большой оси, перпендикулярную к малой оси; в остальном построение эллипса аналогично указанному на чертеже II, б. Малая ось эллипса расположена по направлению не лежащей в данной плоскости аксонометрической оси х', а большая перпендикулярна ей.
III, в. Показан пример применения изометрической проекции окружности, лежащей в профильной плоскости, при изображении цилиндра. Обычно при выполнении аксонометрических проекций заменяют эллипс очень близким ему по очертанию и размерам овалом, построение которого гораздо проще.
2. Построение овала, заменяющего эллипс (при изображении изометрической проекции окружности). Дана ортогональная проекция окружности, лежащей в плоскости П1 (или в любой горизонтальной плоскости). Из центра O1 и точки N проводим лучи под углом 45°, получаем точку М (фиг.279,а).
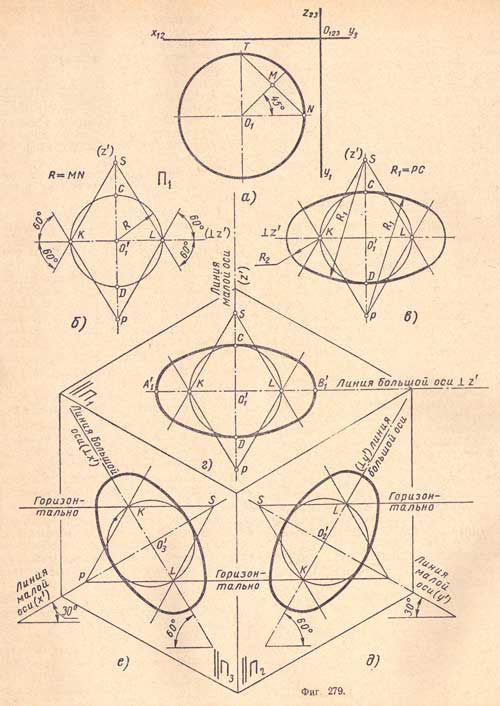
Через намеченную в любом месте точку O'1 проводим линии осей будущего овала (направление малой оси такое же, как и у не лежащей в данной плоскости аксонометрической оси z' , а большой оси - перпендикулярное к малой оси).
Приняв за центр точку O'1, проводим окружность радиусом R = MN (т. е. равным половине хорды TN), получим точки С, D и K, L. Через точки К и L проводим прямые линии под углом 60°, получим точки Р и S (фиг.279,б).
Приняв за центры точки Р и S, проводим дуги радиусом R1 = PC между лучами, выходящими из этих точек (фиг.279,в).
Приняв за центры точки К и L, проводим замыкающие овал дуги радиусом R2, размер которого определяется предыдущим построением (фиг.279,г).
Построение овалов, заменяющих эллипсы при изображении изометрической проекции окружности, лежащей в плоскости проекций П2 или П3, аналогично указанному; причем большая ось овала будет наклонена на угол 60° в первом случае (П2) вправо, а во втором (П3) - влево (фиг.279, д и е).
3. Построение овалов, заменяющих эллипсы при изображении диметрических проекций окружности (фиг.280).
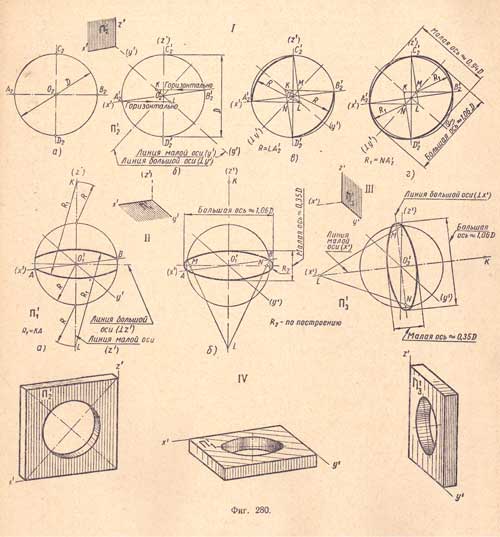
I, а. Дана окружность диаметра D, расположенная в плоскости П2 (или в любой фронтальной плоскости).
I, б. Через намеченную точку O'2, диметриче-скую проекцию точки О2, проводим линии, параллельные осям z' и х', а также линию малой оси в направлении оси у' и линию большой оси в направлении, перпендикулярном к оси у'.
Из центра O'2 проводим вспомогательную окружность диаметром D данной окружности; в пересечении получим точки А'2, В'2, С'2 и D'2 Из точек А'2 и В'2 проводим горизонтальные лучи до пересечения с линией малой оси, получим точки К и L.
I, в. Соединяем отрезками прямых точки К и D'2, а также точки L и С'2, получаем точки М и N. Приняв за центр точку L, радиусом R = LA'2, проводим дугу между точками А'2 и С'2 приняв за центр точку К, тем же радиусом проводим дугу между точками В'2 и D'2
I, г. Приняв за центры точки М и N, проводим радиусом R1 = NA'2 замыкающие овал дуги.
Если данная окружность будет расположена в плоскости П1 (или в любой горизонтальной плоскости), то построение упрощенного очертания ее диметрической проекции (овала) рекомендуется выполнять в такой последовательности:
II, а. Через намеченную точку О'1 проводим прямые линии параллельно диметрическим осям х' и у', а также линию малой оси овала по направлению диметрической оси z' и перпендикулярно линию большой оси овала. Из центра О'1 проводим вспомогательную окружность радиусом R данной окружности, получаем точки А и В; на вертикальной центровой на расстоянии радиуса R выше и ниже проведенной окружности намечаем точки К и L; приняв эти точки за центры, проводим радиусом R1 = КA дуги внутри окружности;
II, б. Точку L соединяем отрезками прямых с концами верхней дуги, на линии большой оси получим точки М и N; приняв их за центры, проводим замыкающие овал дуги.
III. На данном чертеже показано построение овала приближенного очертания диметрическои проекции окружности, расположенной в профильной плоскости, которое выполняется аналогично предыдущему построению.
IV. На чертеже показано изображение овалов на диметрических проекциях детали (квадратной планки с круглым отверстием).
Построение аксонометрических проекций различных геометрических тел (полных, усеченных и пересекающихся) показано на последующих фигурах вместе с построением ортогональных проекций этих тел.











