Парабола.
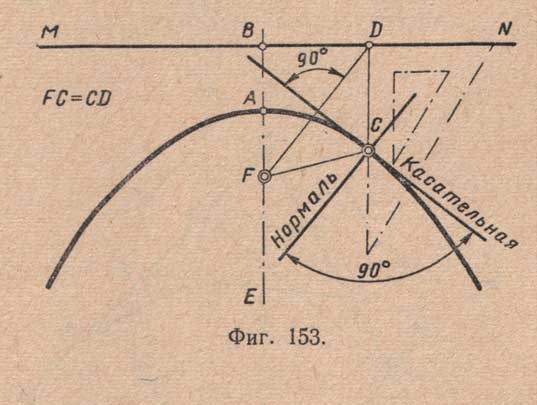
Параболой (фиг.153) называется плоская разомкнутая кривая — геометрическое место точек, одинаково удаленных от данных: точки F и прямой MN (не проходящей через точку F). Например, для точки С FC = CD.
Точка F называется фокусом параболы; прямая MN - направляющей (директрисой); прямая BE, проведенная через точку F перпендикулярно MN, называется осью параболы; точка А, лежащая на середине отрезка BF - оси параболы, заключенного между фокусом F и направляющей MN, называется вершиной параболы. Отрезок, соединяющий любую точку параболы С с ее фокусом F, называется радиусом - вектором параболы; биссектриса угла FCD, составленного перпендикуляром CD, проведенным из любой точки С параболы к направляющей, и радиусом - вектором FC той же точки С, называется касательной в точке С (касательная перпендикулярна отрезку FD); прямая, проведенная через точку С перпендикулярно касательной, называется нормалью.
Построение параболы.
Построение параболы может быть выполнено различными способами:
1) по заданным фокусу F и направляющей MN;
2) по двум заданным в точках К и L касательным к параболе.
Построение параболы по заданным фокусу F и направляющей MN. Через фокус F проводят ось параболы перпендикулярно направляющей MN - получают точку В (фиг.154,а). Отрезок FB делят пополам - получают точку А — вершину параболы; от нее на оси по направлению к фокусу F откладывают несколько произвольных, постепенно увеличивающихся отрезков 1 - 2; 2 - 3 и т. д. Через точки 1, 2, 3 и т. д. проводят прямые, параллельные направляющей MN.
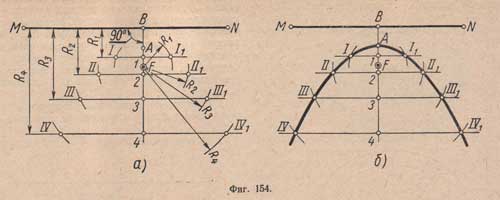
Приняв за центр точку F радиусом R1 = 1B делают засечки I и I1 на первой параллельной прямой, проведенной через точку 1 радиусом R2 = 2B делают засечки II и II1 на второй параллельной прямой, проведенной через точку 2, и т. д. Полученные точки I, I1, II, II1 и т.д. принадлежат параболе.
Через полученные точки проводят кривую - искомую параболу (фиг.154,б).
Построение параболы по двум заданным касательным к ней в точках К и L. Касательные образуют угол KAL, стороны которого КА и AL делят на одинаковое число равных частей. Полученные одноименные точки деления соединяют прямыми (фиг.155,а). В получившуюся внутри угла ломаную линию вписывают кривую - параболу (фиг.155,б).
На (фиг.156,а) изображен корпус крана. Ось трубы крана и линии контурного очертания трубы являются параболами (фиг.156,б).











