Сечение многогранников плоскостью.
Плоская фигура, полученная при пересечении любого многогранника плоскостью, представляет собой некоторый многоугольник. Вершины этого многоугольника находятся как точки пересечения ребер многогранника с секущей плоскостью, а стороны многоугольника строятся как линии пересечения граней многогранника с секущей плоскостью.
Сечение призмы проектирующей плоскостью (фиг. 302).
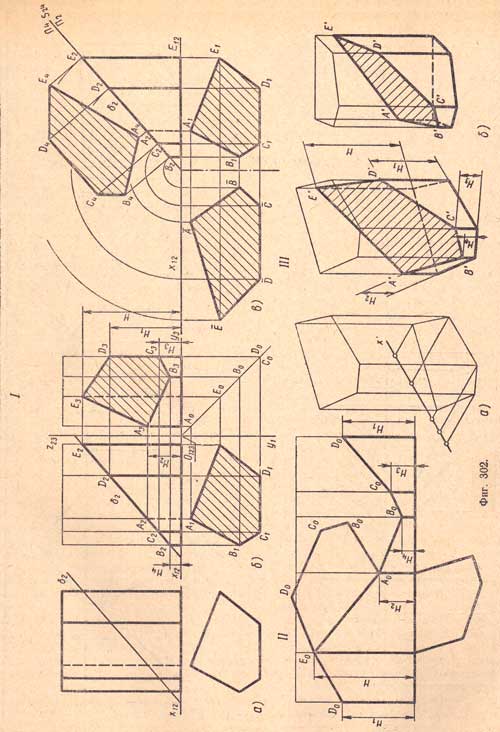
I, а. Пятиугольная прямая призма поставлена основанием на плоскость П1 и рассечена фронтально-проектирующей плоскостью δ.
Требуется:
а) построить проекции сечения;
б) найти натуральную величину фигуры сечения;
в) построить развертку поверхности усеченной призмы;
г) построить аксонометрическую проекцию усеченной призмы.
I, б. Нахождение проекций сечений. Фронтальная проекция В2С2А2D2Е2 фигуры сечения совпадает с фронтальной проекцией δ2 плоскости δ, так как вершины фигуры сечения являются точками пересечения ребер призмы с плоскостью δ. Горизонтальная проекция фигуры сечения совпадает с горизонтальной проекцией призмы, так как призма прямая и ее ребра и грани перпендикулярны плоскости П1. Профильная проекция фигуры сечения выявится многоугольником, полученным путем построения третьей проекции по двум данным.
I, в. Нахождение натуральной величины фигуры сечения.
а) Метод совмещения. Совместим плоскость δ с плоскостью П1. За ось вращения принимаем горизонтальный след плоскости δ. Проекция δ2 совместится с осью х12. Пользуясь правилом совмещения, находим натуральную величину фигуры сечения ¯A¯B¯C¯D¯E.
б) Метод перемены плоскостей проекций. Принимаем плоскость δ за новую плоскость проекций, а проекцию δ2 - за новую ось проекций s24. Проводим из проекций B2C2A2D2 и Е2 перпендикуляры к новой оси s24 и на них откладываем глубины вершин фигуры сечения, например: E2E4 = E1E4 и т.д. Точки A4, B4, С4, D4, E4 последовательно соединяем прямыми и получаем натуральную величину фигуры сечения.
Фигуру сечения и ее проекции на чертеже выделяют штриховкой под углом 45° к оси х12.
Штриховка может быть наклонена как вправо, так и влево, но для всех проекций и фигуры сечения штриховку следует выполнять в одну сторону.
II. Построение развертки поверхности усеченной призмы. Строим развертку боковой поверхности данной призмы. Затем на соответствующих боковых ребрах откладываем размеры оставшихся после отсечения плоскостью частей ребер H, Н1, Н2, H3 и Н4, которые берем с фронтальной и профильной проекций. Соединив последовательно прямыми точки DO, ЕO, АO, ВO, СO, DO, получим линию сечения, по которой плоскость δ рассекает призму на две части. Для получения развертки поверхности усеченной призмы к соответствующим боковым граням пристраиваем фигуру сечения и нижнее основание.
III. Построение аксонометрических проекций усеченной призмы.
III, а. Строим аксонометрическую проекцию призмы, пользуясь координатами на (фиг.302, I, а).
III, б. На соответствующих ребрах боковых граней откладываем от нижнего основания оставшиеся части ребер, используя для этого размеры Н, Н1, Н3, Н3, H4.
Полученные точки А', В', С, D', Е' и А' соединяем прямыми. Определяем невидимые и видимые элементы и обводим их соответствующими линиями.
Сечение призмы плоскостью общего положения (фиг.303).
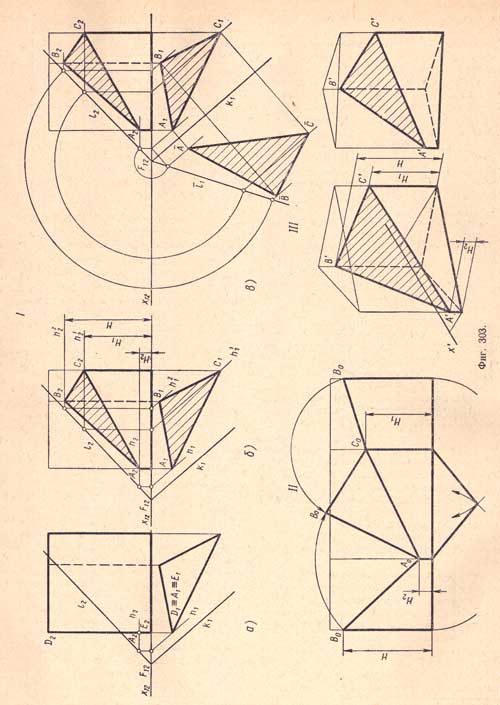
I, а. Треугольная прямая призма поставлена основанием на плоскость П1 и рассечена плоскостью а общего положения.
Требуется:
а) построить проекции сечения;
б) найти натуральную величину фигуры сечения;
в) построить развертку поверхности усеченной призмы;
г) построить аксонометрическую проекцию усеченной призмы.
В этом случае горизонтальная проекция фигуры сечения сливается с горизонтальной проекцией призмы, так как боковые ребра и грани призмы перпендикулярны плоскости П1. Для построения фронтальной проекции воспользуемся горизонталями. Через точку А1 - горизонтальную проекцию ребра - проводим прямую, параллельную проекции следа k1 - горизонтальную проекцию h1 горизонтали. Затем найдем ее фронтальную проекцию h2, которая, пересекаясь с фронтальной проекцией ребра D2E2 в точке А2 определит фронтальную проекцию точки пересечения ребра призмы с плоскостью а.
I, б. Аналогичным построением находим остальные точки пересечения ребер призмы плоскостью а (В2, С2), после чего соединим последовательно прямыми точки А2, В2, С2 и А2 и получим фронтальную проекцию А2В2С2 фигуры сечения - треугольника.
I, в. Натуральную величину фигуры сечения находим путем совмещения плоскости а с плоскостью П1 вращением вокруг проекции следа k1
II и III. Построение развертки поверхности усеченной призмы и аксонометрических проекций аналогично соответствующим построениям для пятиугольной призмы (фиг.302).
Сечение пирамиды фронтально - проектирующей плоскостью (фиг. 304).
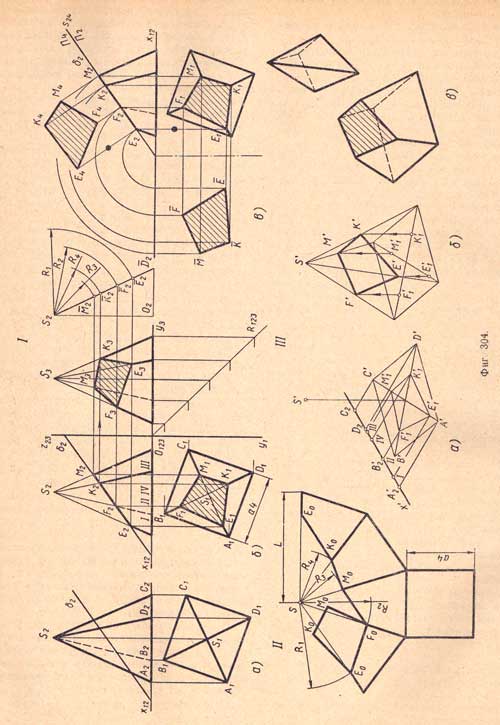
1, а. Правильная четырехугольная пирамида поставлена основанием на плоскость П1 и рассечена фронтально-проектирующей плоскостью б.
Требуется:
а) построить проекции сечения;
б) найти натуральную величину фигуры сечения;
в) построить развертку поверхности усеченной пирамиды;
г) построить аксонометрическую проекцию усеченной пирамиды (фиг.304, а).
I. б. Фронтальная проекция фигуры сечения - отрезок E2F2К2М2 - совпадает с фронтальной проекцией δ2 так как точки пересечения ребер пирамиды с секущей плоскостью лежат в плоскости δ.
Горизонтальные проекции точек пересечения находят при помощи вертикальных линий связи на горизонтальных проекциях соответствующих ребер, например: точку Е1 на горизонтальной проекции ребра S1A1, точку F1 на S1B1 и т.д.
Соединив последовательно прямыми точки Къ Ei, &i, JWi и Кг, получим горизонтальную проекцию фигуры сечения.
Профильная проекция фигуры сечения - четырехугольник E3F3M3K3 находится, как третья проекция, по двум данным (фиг.304,б).
I. в. Натуральная величина фигуры сечения находится способом совмещения плоскости δ с плоскостью П1 и способом перемены плоскостей проекций, где за новую плоскость П4 принята плоскость δ, а за новую ось проекций S24 - проекция δ2 (фиг.304,в).
II. Для построения развертки боковой поверхности находим натуральную величину ребра пирамиды путем построения прямоугольного треугольника S2O2¯D2, у которого S2O2 = H, a O2¯D2 = S1¯D1; гипотенуза S2D2 является натуральной величиной ребра. Зто равносильно повороту ребра до параллельности плоскости П2. Затем строим развертку боковой поверхности нерассеченной пирамиды - фигуру, состоящую из четырех равнобедренных треугольников, основания которых равны сторонам квадрата основания, а боковые стороны - натуральным величинам ребер.
Для определения величины отсеченных частей ребер, вместо поворота их, переносим с профильной проекции на натуральную величину ребра точки E3,F3,M3 и К3, получаем размеры R1,R2,R3,R4 Равные отсеченным частям ребер размер R1 равен отсеченной части S2¯E2, R2 равен S2¯F2 и т. д. (фиг.304, I, б).
Перенеся на развертку при помощи этих размеров на соответствующие ребра точки Ео, Fo, Мо, Ко и Ео и соединив их последовательно прямыми, получим ломаную линию, по которой пирамида рассечена фронтально-проектирующей плоскостью δ. Для получения развертки поверхности усеченной пирамиды к линии сечения присоединяем соответствующей стороной фигуру сечения, а к линии основания — основание пирамиды.
III, а. Для изображения изометрической проекции усеченной пирамиды, пользуясь координатами с (фиг.304, I, б), сначала строим основание и вершину пирамиды, а затем вторичную проекцию фигуры сечения (горизонтальную проекцию фигуры сечения) E'1F'1M'1K'1.
III, б. Соединяем прямыми точку S' (вершину пирамиды) с точками А', В', С и D' (вершинами основания) - получаем изометрическую проекцию пирамиды.
Из точек Е'1, F'1, M'1 и К'1 параллельно оси z проводим прямые до пересечения с соответствующими ребрами пирамиды. Точки Е'1, F'1, M'1 и К'1 явятся вершинами фигуры сечения, соединив которые прямыми, получим изометрическую проекцию фигуры сечения.
III, в. Определив видимые и невидимые элементы усеченной призмы, обводим их соответствующими линиями и заштриховываем фигуру сечения. Над усеченной частью пирамиды изображена отсеченная ее часть.
Сечение тел вращения плоскостью.....











