Эллипс.
Эллипсом называется плоская замкнутая кривая — геометрическое место точек, сумма расстояний от которых до заданных точек F1 и F2 равняется длине заданного отрезка АВ, проведенного через точки F1 и F2 так, чтобы отрезок AF1 равнялся отрезку F2B (фиг. 148); например, для точки К расстояния F1К + KF2 = АВ. Отрезок АВ называется большой осью эллипса, а точки F1 и F2 — фокусами эллипса. Отрезок CD, проведенный через середину большой оси - точку О - центр эллипса перпендикулярно к ней, называется малой осью эллипса. Биссектриса угла F1KF2 называется нормалью эллипса, а биссектриса смежного с ним угла F2KM называется касательной эллипса. Нормаль перпендикулярна касательной. (Точка К. может находиться в любом месте эллипса).
1. Образование эллипса.
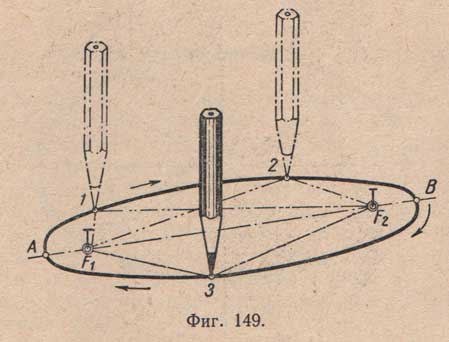
На (фиг.149) показано приспособление, при помощи которого легко уяснить образование эллипса. На бумаге проводят прямую линию и намечают на ней две точки F1 и F2 затем берут нить и на ее концах делают петли с таким расчетом, чтобы длина нити . с петлями равнялась большой оси АВ будущего эллипса. Петли надевают на булавки, закрепленные в двух данных точках-фокусах F1 и F2. Натянув нить конической частью карандаша, проводят очерк эллипса. Во всех показанных положениях сумма двух отрезков нити равна всей длине нити, которая, как было сказано, равняется большой оси АВ, т. е. F11 + 1F2 = F12 + 2F2 = F13 + 3F2 = AB
2. Построение эллипса.
Построение эллипса может быть выполнено различными способами: по заданным двум осям эллипса и по заданным сопряженным диаметрам.
Построение эллипса по двум заданным его осям. На (фиг.150,a) показано построение для нахождения любых точек М и N, принадлежащих эллипсу.
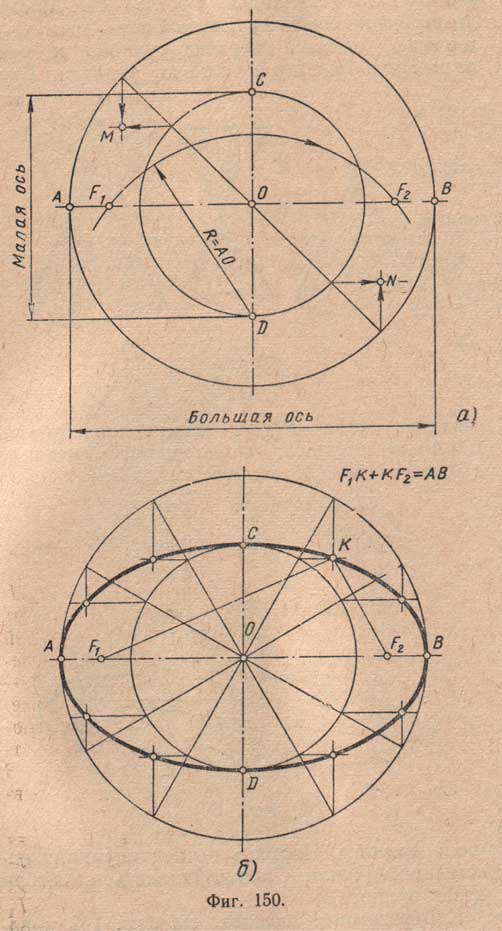
Для этого проводят две концентрические окружности, диаметры которых равны большой АВ и малой CD осям будущего эллипса и в любом направлении диаметр большой окружности. Из точек его пересечения с большой окружностью проводят лучи параллельно малой оси, а из точек пересечения с малой окружностью - параллельно большой оси.
Точки М и N пересечения этих лучей явятся точками эллипса. Для нахождения фокусов F1 и F2 надо из точки D, как из центра, провести дугу радиусом R = АО; она пересечет ось АВ в точках F1 и F2 (фокусах).
На (фиг.150,б) показаны аналогичные построения для нахождения ряда точек, принадлежащих эллипсу (в данном случае 12 точек). Проведенная через них замкнутая кривая явится эллипсом.
Построение эллипса по заданным сопряженным диаметрам. Аналогично окружности внутри эллипса можно провести хорды, причем хорды, проведенные через центр О эллипса, называются его диаметрами.
Если каждый из двух диаметров эллипса делит пополам,хорды, параллельные другому диаметру, то такие диаметры называются сопряженными.
На (фиг.151) показаны построения для нахождения точек эллипса по заданным сопряженным диаметрам АВ и CD.
Отрезок АО = AB / 2 Делят на некоторое число равных частей, например на 4; получают точки I, II, III ; отрезок АК = CD / 2 делят на столько же частей - получают точки 1, 2, 3. Точку С соединяют с точками 1, 2 и 3, а из точки D проводят лучи через точки I, II и III до пересечения с одноименными отрезками. Точки пересечения явятся точками, принадлежащими одной четверти эллипса. Аналогичные точки эллипса на других четвертях находят, как симметричные относительно диаметров АВ и CD.
3. Пример детали эксцентрик. Эксцентрика, имеющий очертания эллипса, показан на (фиг.152, а).
На (фиг.152,б) показан контур эксцентрика (эллипс).











