Построение аксонометрических проекций.
Построение аксонометрических проекций точки, отрезка и фигуры
1. Построение аксонометрических осей координат. Аксонометрические оси х' и у' для изометрической и кабинетной проекций наклонены по отношению к горизонтальной линии на углы в 30 и 45° и не требуют объяснений для их построения.
Построение аксонометрической оси х для диметрической проекции, наклоненной на угол 7°10', и оси у', наклоненной на угол 41° 25', рекомендуется выполнять в такой последовательности:
а) намечают точку О' - начало координат; проводят аксонометрическую ось z (вертикально); приняв за центр точку О', проводят слева дугу произвольного радиуса R, получают точку А (фиг.273,а).
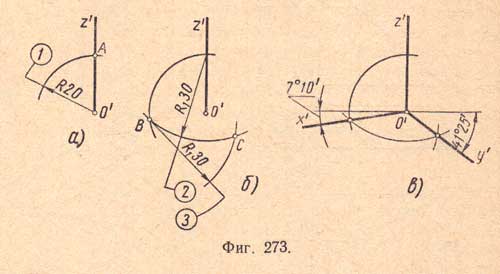
б) приняв за центр точку А, проводят дугу R1 - 1,5R, получают точку В; приняв за центр точку В, проводят дугу тем же радиусом R1 и получают точку С (фиг.273,б);
в) из точки О' проводят лучи через точки В и С (фиг.273,в). Эти лучи явятся аксонометрическими осями х' (7° 10') и у' (41° 25').
2. Построение аксонометрической проекции точки. Даны ортогональные проекции A1, A2, А3 точки А (фиг.274,a) (координаты х =20, у = 30, z = 40).
Для построения изометрической проекции точки А:
1) проводят аксонометрические оси координат х', у' и z'; откладывают по аксонометрической оси х' абсциссу (20) точки А; затем из полученной точки А'х проводят луч параллельно аксонометрической оси у' и на нем откладывают ординату (30) точки А; точка А1 явится вторичной горизонтальной проекцией точки А1 (фиг.274,а); вторичными проекциями называют аксонометрические проекции проекций геометрических элементов на координатные плоскости.
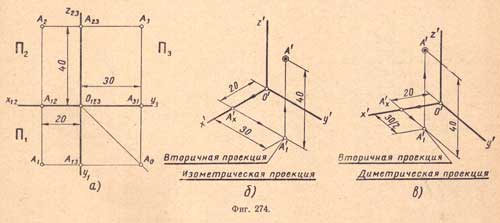
2) из точки А'1 проводят луч параллельно аксонометрической оси z' на высоту аппликаты (40) - получают точку А' - изометрическую проекцию точки А (фиг.274,б).
Примечания:
1. Построение аксонометрической проекции точки можно начинать по любой аксонометрической оси координат.
2. Приемы построения диметрической проекции точки аналогичны указанному (см. фиг. 274, в).
3. Если данная точка лежит в плоскости проекций, то ее аксонометрическая проекция сливается с вторичной проекцией.
3. Построение аксонометрической проекции отрезка. Даны ортогональные проекции А1В1 и А2В2 отрезка АВ (фиг.275,а):
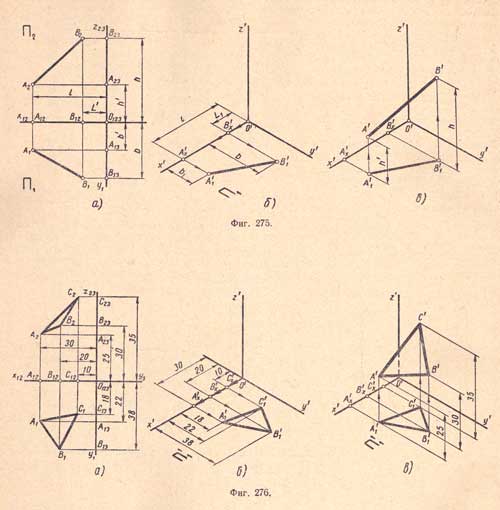
1) согласно координатам конечных точек А и В строим их вторичные проекции на плоскости П'1 соединяя точки А'1 и В'1 отрезком прямой, получим на плоскости П'1 вторичную проекцию A'1B'1 данного отрезка (фиг.275,б);
2) из точек А'1 и В'1 проводим параллельно аксонометрической оси z' лучи (фиг.275,в), на которых, откладывая аппликаты точек А и В, получаем изометрические проекции А' и В' конечных точек отрезка АВ; соединив их отрезком прямой, получаем изометрическую проекцию А'В' отрезка АВ (диметрическая и кабинетная проекции отрезка выполняются аналогично показанной изометрической проекции).
4. Построение аксонометрической проекции плоской фигуры (треугольника) по комплексному чертежу. Дано: проекции А1В1С1 и А2В2С2 треугольника ABC (фиг.276,а):
1) строим на плоскости П1 вторичные изометрические проекции вершин А, В и С; соединяя их отрезками прямых, получаем вторичную проекцию A'1B'1C'1 данного треугольника (фиг.276,б);
2) из точек А'1, В'1 и С'1, проводим лучи параллельно аксонометрической оси г на высоту их аппликат; получаем точки А', В' и С, соединив которые отрезками прямых, получим изометрическую проекцию А'В'С' треугольника ABC (фиг.276,в).
Построение аксонометрической проекции фигуры произвольного очертания, лежащей в плоскости П1.
Даны ортогональные проекции A1B1C1D1G1 и A2B2C2D2G2 фигуры произвольного очертания.
Для построения изометрической проекции участка контура, имеющего криволинейное очертание, намечаем на нем несколько точек, например E1 и F1. Определяем координаты всех указанных точек (фиг.277,а)
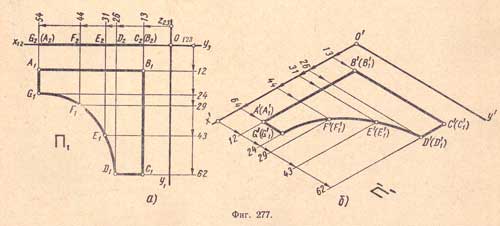
пользуясь этими координатами, строим на плоскости П1 вторичную проекцию A'1B'1C'1D'1E'1F'1G'1, которая вместе с тем явится и изометрической проекцией A'B'C'D'E'F'G' данной фигуры (фиг.277,б).
Аксонометрическая проекция окружности.....











