Гипербола.
Гиперболой называется плоская разомкнутая кривая - геометрическое место точек, разность расстояний которых от данных точек F1 и F2 равняется заданному отрезку АВ. Гипербола имеет две симметричные ветви (фиг.157).
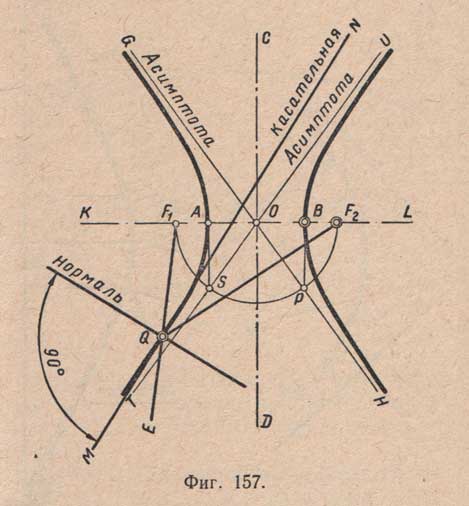
Прямая, проходящая через точки А и В - вершины гиперболы, называется действительной осью, а середина отрезка АВ (точка О) называется центром гиперболы; прямая CD, проведенная через центр О перпендикулярно действительной оси АВ, называется мнимой осью. Точки F1 и F2, лежащие симметрично (относительно мнимой оси) на действительной оси, называются фокусами гиперболы. Биссектриса MN угла F1QF2 (точка Q взята произвольно на гиперболе) является касательной к гиперболе в точке Q а биссектриса смежного угла EQF2 - нормалью. Касательная перпендикулярна нормали.
Касательные к гиперболе, точки касания которых удалены от вершины на бесконечное расстояние, называются асимптотами (TU и GH). Для их построения проводят из вершин А и В прямые, параллельные мнимой оси, до пересечения с полуокружностью, проведенной из центра О радиусом OF1
Через полученные точки S и Р и центр О проводят прямые - асимптоты. Если асимптоты взаимно-перпендикулярны, то гиперболу называют равнобокой.
Построение гиперболы. Из различных приемов построения гиперболы ниже приведены два случая.
Построение гиперболы по заданным вершинам А и В и фокусному расстоянию F1F2.
Проводят прямую и намечают на ней заданные вершины А и В и фокусы F1 и F2 (фиг.158,а); левее фокуса F1 откладывают некоторое количество произвольных, постепенно увеличивающихся отрезков 1 - 2, 2 - 3 и т. д. Приняв за центры фокусы F1 и F2, проводят две дуги радиусом R1 = 1B, затем из тех же центров проводят две дуги радиусом R1 = 1A. В результате получают четыре точки пересечения, которые обозначают I, I, I1 и I1.
Из тех же центров F1 и F2 проводят дуги радиусами R2 - 2B и R3 = ЗВ и пересекают их дугами, проведенными из тех же центров радиусами R'2 = 2А и R'3 = ЗА (фиг.158,б).
Через полученные точки пересечения и вершину гиперболы (т. е. через точки III1, II1, I1, А, I1, II1, III1) проводят кривую - одну ветвь гиперболы, а через точки III, II, I, В, I, II, III - кривую - вторую ветвь гиперболы.
Построение равнобокой гиперболы по заданным асимптотам и точке К, принадлежащей гиперболе.
Через данную точку К проводят вспомогательные прямые, параллельные заданным асимптотам (фиг.159,а).
Из точки О проводят произвольно наклоненные лучи. Из точек их пересечения с вспомогательными прямыми проводят навстречу одна другой прямые, параллельные асимптотам. Точки L и М их пересечения явятся точками, принадлежащими гиперболе (фиг.159,б).
Кривая, проведенная через точки L, К и М, явится искомой гиперболой (фиг.159,в).
На (фиг.160) показана кривая, полученная в результате разреза отражателя, которая является гиперболой.











