Коническая поверхность.

Конической поверхностью называется поверхность, образуемая движением прямой (AВ), перемещающейся в пространстве так, что она при этом постоянно проходит через неподвижную точку S и пересекает данную линию MN (фиг.294).

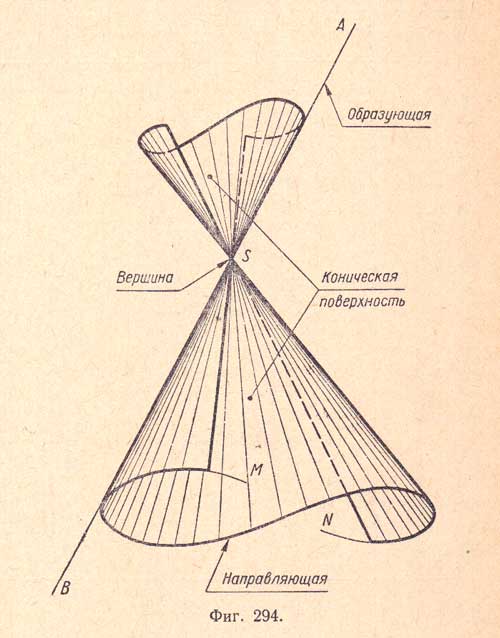
Прямая АВ называется образующей, линия MN - направляющей, а точка S - вершиной конической поверхности.
1. Конус.
Конусом называют тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины, и плоскостью, пересекающей все образующие. Часть конической поверхности, ограниченная этой плоскостью, называется боковой поверхностью, а часть плоскости, отсекаемая боковой поверхностью, - основанием конуса. Перпендикуляр, опущенный из вершины на плоскость основания, называется высотой конуса (фиг.295,а).

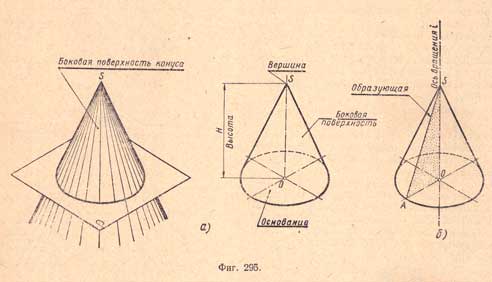
Конус называется прямым круговым, если его основание - круг, а высота проходит через центр основания. Такой конус можно рассматривать как тело, полученное вращением прямоугольного треугольника SAO вокруг катета SO, как оси. При этом гипотенуза SA описывает боковую поверхность, а катет АО - основание конуса (фиг.295,б).
Если ось вращения прямого кругового конуса параллельна плоскости проекций, то проекция конуса на эту плоскость является треугольником (равнобедренным или равносторонним), основание которого будет равно диаметру основания конуса, а стороны - образующей конуса.
Если ось вращения конуса перпендикулярна плоскости проекций, то проекция конуса на эту плоскость будет кругом, равным натуральной величине основания конуса. В этом случае образующие на проекции не изображаются.
2. Изображение прямого кругового конуса (фиг.296).

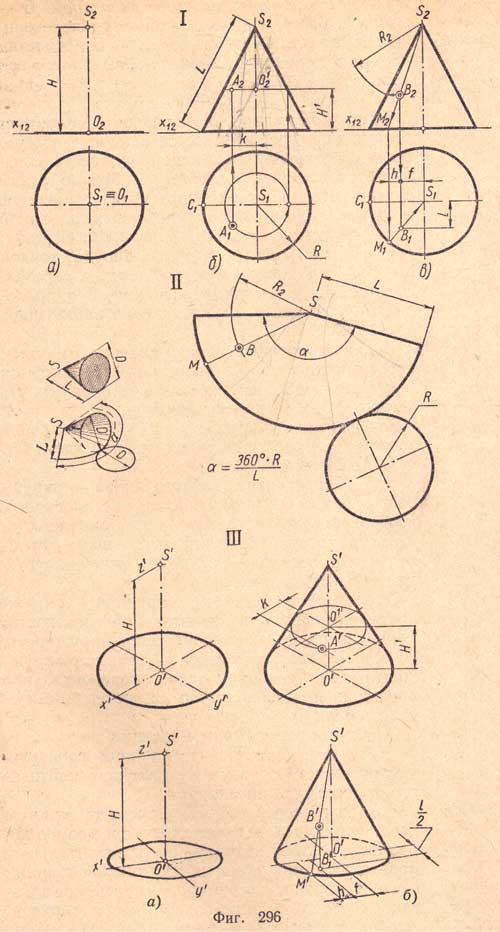
Дано: основание конуса, расположенного на плоскости П₁
I. Комплексный чертеж
I, а. Проектируем основание конуса - круг, расположенный в плоскости П₁, и вершину конуса - точку S, расположенную в пространстве на вертикальной прямой, проходящей через центр основания. Высота точки S равна высоте конуса. Горизонтальная проекция этой точки находится в центре окружности - горизонтальной проекции основания.
I, б. Проектируем боковую поверхность конуса. Для этого достаточно спроектировать на плоскость П₂ контурные образующие, для чего соединяем прямыми фронтальные проекции вершины S₂ с проекциями крайних точек основания и получаем проекции контурных образующих, а в целом - фронтальную проекцию данного конуса - равнобедренный треугольник, основание которого равно диаметру основания конуса, а высота треугольника - высоте конуса.
На горизонтальной проекции боковой поверхности конуса дана горизонтальная проекция А₁ точки А, требуется найти ее фронтальную проекцию. Для этого на горизонтальной проекции конуса через точку А₁ проводим окружность - горизонтальную проекцию параллели, затем находим ее фронтальную проекцию и при помощи вертикальной линии связи (направление которой на чертеже показано стрелкой) находим фронтальную проекцию A₂ точки A.

I. в. Эту задачу можно решить и при помощи образующей. На фронтальной проекции боковой поверхности конуса дана фронтальная проекция В₂ точки В. Из точки S₂ через точку В₂ проводим прямую S₂М₂ - проекцию образующей конуса, затем находим ее горизонтальную проекцию S₁М₁ и на ней при помощи вертикальной линии связи определяем место горизонтальной проекции точки В.
II. Развертка поверхности прямого кругового конуса - плоская фигура, составленная из сектора и окружности, диаметр которой равен диаметру окружности основания. Радиусом сек-гора является образующая конуса, а длина дуги равна длине окружности основания конуса. Угол сектора можно определить по формуле (a =360°R ÷ L) где R - радиус окружности основания конуса; L - образующая конуса. При построении развертки следует придерживаться следующего порядка:
а) определить угол а сектора;
б) построить развертку боковой поверхности конуса - сектор;
в) пристроить к любой точке, дуги сектора основание конуса - круг.
Перенос точки В на развертку боковой поверхности конуса осуществляется при помощи размеров С₁М₁ и R₂, взятых с (фиг.296, I, в).

III. Наглядное изображение конуса в аксонометрии (изометрия и диметрия).
III, а. Изображаем основание конуса - овал по данному условию. Через центр основания проводим ось z' и на ней от точки О' откладываем высоту конуса О'S', получаем его вершину S'.
III, б. Изображаем контурные образующие. Из точки S' проводим прямые, касательные к овалу, получаем изображение конуса. Невидимую часть основания (половину овала) изображаем штриховыми линиями.
Определение точки А на боковой поверхности осуществляем при помощи нанесения на поверхность конуса параллели, диаметр параллели берем с горизонтальной проекции (фиг.296, I, б), а ее центр О₂ определяем размером H₁, с фронтальной проекции (фиг.296, I, б). Место точки А на параллели определяется пересечением вспомогательной прямой, проведенной на расстоянии k параллельно оси у' с параллелью.
Определение точки В на боковой поверхности конуса осуществляется:
а) нанесением на коническую поверхность образующей S'M' при помощи размеров h и f;
б) нахождением вторичной проекции В₁ точки В при помощи размера i/2;
в) проведением вспомогательной прямой из точки В'₁ параллельно оси вращения S'O'. Пересечение вспомогательной прямой с образующей конуса определяют место точки В'.
Определить места точек А и В на боковой поверхности конуса можно и при помощи координат.
ТОР
Тело, полученное от вращения окружности (эта окружность называется образующей) вокруг оси, расположенной в плоскости этой окружности, но не проходящей через ее центр, называется ТОРОМ. Если ось вращения. не пересекает окружность, то тор называют кольцом (фиг.297). Изображение кольца (фиг.298).

1. Комплексный чертеж
I, а. Дано: ось кольца перпендикулярна плоскости П₁( диаметр D образующей окружности кольца и диаметр D_ц окружности центров образующих окружностей (фиг.298,а).
I, б. Горизонтальная проекция кольца выявится двумя концентрическими окружностями (фиг.298,б) диаметр большей равен D_ц+ D; диаметр меньшей Dц - D. Фронтальная проекция выявится двумя образующими окружностями, сопряженными прямыми.
Заметим, что внутренние половины окружностей необходимо изобразить штриховыми линиями, как невидимые.
I, в. Дано: горизонтальные проекции параллелей и на них проекции двух точек: точки А (A₁) на малой параллели; точки В (B₂) на большой (фиг.298,в). Требуется найти их фронтальные проекции. Для этого сначала надо найти фронтальные проекции параллелей, а затем при помощи вертикальных линий связи определить на них места фронтальных проекций А₂ и В₂.
II. Наглядное изображение кольца в изометрии и диметрии.
II, а. Изооражаем место центров сфер - окружность (D'_ц), расположенную в горизонтальной плоскости.
II, б. Изображаем контур поверхности кольца при помощи вспомогательных сфер, для чего проводим ряд окружностей диаметром D - контуров сфер, центры которых расположены на окружности центров. Затем к окружностям проводим плавную касательную, выявляя очерк кольца.
ШАР
Тело, полученное от вращения полукруга вокруг диаметра, называется шаром, а поверхность, образуемая при этом окружностью, называется шаровой или сферой. Можно также сказать, что эта поверхность есть геометрическое место точек, одинаково удаленных от одной и той же точки, называемой центром. Отрезок, соединяющий центр с какой-нибудь точкой поверхности, называется радиусом, а отрезок, соединяющий две точки поверхности и проходящий через центр, называется диаметром шара (фиг.299).
Всякая проекция шара является кругом, очерками проекций на плоскость П₁ является проекция экватора, на плоскость П₂ и П₃ являются проекции меридианов.
Изображение шара (фиг.300). Дано: одной точкой поверхности шар касается плоскости П₁.
I. Комплексный чертеж
I, а. Проектируем экватор шара - окружность, лежащую в горизонтальной плоскости, горизонтальная проекция - это окружность, диаметр которой равен диаметру шара. Фронтальная проекция - прямая (обычно на чертеже не изображается).
Проектируем главный меридиан - окружность, лежащую в фронтальной плоскости; фронтальной проекцией является окружность, по условию касательная оси х₁₂; диаметр окружности равен диаметру шара, горизонтальная проекция прямая (обычно на чертеже не изображаемая).
В результате получим проекции шара.
I, б. На поверхности шара дана фронтальная проекция А₂ точки А, требуется найти ее горизонтальную проекцию.
Для этого через точку А₂ проведем прямую параллельно оси - фронтальную проекцию параллели, затем находим ее горизонтальную проекцию и при помощи вертикальной линии связи (направление которой на чертеже показано стрелкой) определяем место горизонтальной проекции А₁ точки А. Развертка поверхности шара. Развертка может быть построена только приближенно, так как шаровая поверхность (сфера) принадлежит к поверхностям неразвертывающимся.
Построение развертки будем выполнять методом долей (существуют и другие методы).
I, в. Для этого фронтальную проекцию главного меридиана - окружность - делим на 12 равных чаетей, каждая часть деления будет равна ¹/_{12 п}D (т.е.¹/₁₂ меридиана). Через точки деления 1, 2 и 3 проводим прямые, параллельные оси x₁₂ - проекции параллелей, и находим их горизонтальные проекции - окружности. D_П1 - первая параллель; D_П2 - вторая параллель и D_Э - экватор. Затем горизонтальную проекцию экватора - окружность D_Э - делим на 12 равных частей, каждая часть деления будет равна ( ¹/_{12 П}D_Э) (т.е. ¹/₁₂ экватора); через каждое деление экватора проводим меридиональные плоскости, которые разделяют поверхность шара, а следовательно, и каждую параллель на 12 долей; получим части параллелей ¹/_{12 П}D_П1 и ¹/_{12 П}D_П2
II. Построение одной доли. Проводим прямую O¹O², равную (_ПD_M ÷ 2) и от точки О¹ откладываем три раза части, равные ( _ПD_M ÷ 12 ), и через каждую часть проводим прямые, перпендикулярные к O¹O², на которых откладываем отрезки: (3 - 3 = _ПD_Э ÷ 12); (2 - 2 = _ПD_П2 ÷ 12); (2 - 2 = _ПD_П1 ÷ 12), как показано на чертеже. Соединив плавной кривой последовательно точки 3 - 2 - 1 - 0¹ - 1 - 2 - 3, получим половину очертания доли. Построив вторую половину, получим одну долю, т.е. 1/12 часть приближенной развертки поверхности шара. Для получения полной развертки поверхности шара следует построить 12 долей.
III. Наглядное изображение шара в изометрии.
III, а. Изображаем экватор шдра как аксонометрическую проекцию окружности, лежащую в горизонтальной плоскости.
III, б. Точку О' принимаем за центр, проводим окружность (касательную к овалу), получаем изометрическую проекцию шара. Диаметр окружности равен длине овала.
Определение места точки А на шаровой поверхности можно осуществить при помощи параллели. Изображаем на поверхности шара параллель, пользуясь размерами h и D_П место точки на параллели определяем с помощью прямой, проведенной параллельно оси у' на расстоянии k.
Определить точку А на шаровой поверхности можно при помощи координат.
Упражнение
Пример 1.
а) Выполнить комплексные чертежи геометрических тел согласно примерам А, Б и В по данным размерам (фиг.301,а).
б) Примеры A w В выполнить в изометрической проекции, а пример Б в диметрической.
в) На поверхности каждого тела спроектировать произвольно взятую точку.
Пример 2.
Выполнить комплексные чертежи каждого геометрического тела отдельно (фиг.301,б).
Пример 3.
Выполнить комплексные чертежи геометрических тел, составляющих формы некоторых деталей, согласно примеру (фиг.301,в).

Сечение многогранников плоскостью.....