Вращения и развертки поверхностей.

КОМПЛЕКСНЫЙ ЧЕРТЕЖ ТЕЛ ВРАЩЕНИЯ И РАЗВЕРТКИ ИХ ПОВЕРХНОСТЕЙ
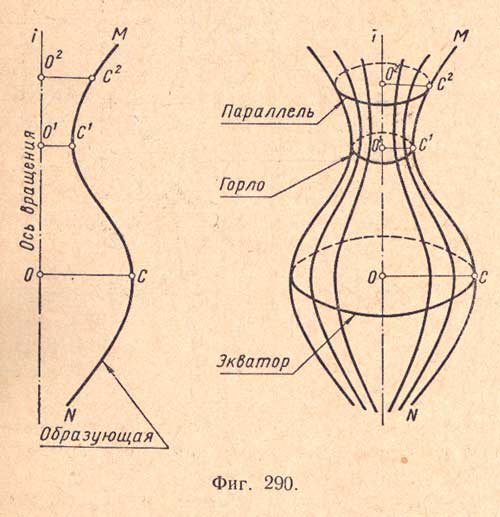
Поверхностью вращения называется поверхность, которая получается от вращения какой - нибудь линии МN (фиг.290,а), называемой образующей, вокруг неподвижной прямой i называемой осью; при этом предполагается, что образующая МN при своем вращении связана с осью i.
Если взять на образующей какую-нибудь точку С и опустить из нес на ось перпендикуляр СО, то очевидно, что при вращении длина перпендикуляра, величина прямого угла iOС и положение точки О не будут изменяться.

Следовательно, каждая точка образующей будет описывать окружность, плоскость которой перпендикулярна оси i, а центр лежит на пересечении этой плоскости с осью. Отсюда следует: линия пересечения плоскости, перпендикулярной к оси, с поверхностью вращения является окружностью.
Каждая точка образующей при движении вокруг оси описывает окружность. Эти окружности называются параллелями. Наибольшая из них называется экватором, а наименьшая - горлом (фиг.290,б).
Всякая секущая плоскость, проходящая через ось, называется меридиональной плоскостью, а линия ее пересечения с поверхностью вращения - меридианом. Все меридианы равны между собой. Если ось вращения параллельна плоскости П₂, а меридиональная плоскость занимает фронтальное положение, то полученный отсечения меридиан проектируется. на плоскость П₂ без искажения; этот меридиан называется главным.

Цилиндрическая поверхность.....