Спираль Архимеда.

Спиралью Архимеда называется плоская кривая, полученная как след точки, движущейся равномерно поступательно от неподвижной точки О по выходящему из нее и равномерно вращающемуся вокруг точки О лучу (радиусу) (фиг.165).

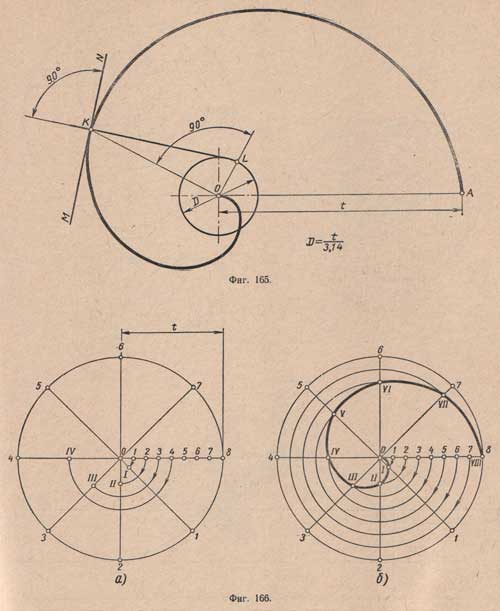
Спиралью Архимеда движущаяся равномерно поступательно от неподвижной точки

Точка О называется полюсом спирали; отрезок ОА называется шагом t спирали; отрезок KL - нормалью спирали, а прямая MN, перпендикулярная к нормали, называется касательной; точка К может
находиться в любом месте спирали, а точку L находят путем построения, для чего точку К соединяют прямой с точкой О и в точке О проводят перпендикуляр к отрезку КО, который пересечет в точке L окружность, проведенную из центра О диаметром D = t/3,14.

Построение спирали Архимеда

Заданный шаг t спирали Архимеда делят на несколько, например на восемь, равных частей (фиг.166,а). Из конца О отрезка / проводят окружность R = t и делят ее на столько же равных частей, на сколько был разделен шаг t.
На первом луче путем проведения дуги радиусом O1 из центра О получают точку I, на втором луче путем проведения дуги радиусом O2 получают точку II и т.д.
После того как на всех лучах будут получены точки I, II, III, IV, V, VI, VII и VIII, проводят через них кривую - спираль Архимеда (фиг. 166, б).
На (фиг.167,а) дано изображение распределительного кулачка. Очертания боковых сторон его выполняют по спирали Архимеда (фиг.167,б).