Определение длины отрезка прямой.
Определение длины отрезка прямой на комплексном чертеже. В пространстве дан отрезок АВ общего положения и его горизонтальная проекция А1 В1 (фиг.209).
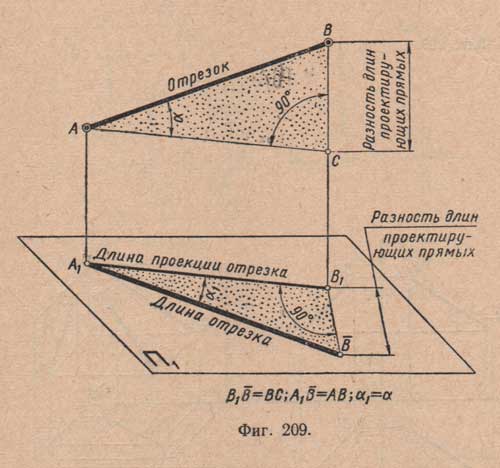
Проведем через точку А перпендикуляр к проектирующей прямой ВВ1, получим прямоугольный треугольник ABC, у которого один катет ВС равен разности проектирующих прямых (ВС = ВВ1 - AA1), другой катет равен горизонтальной проекции А1В1, а гипотенуза равна проектируемому отрезку АВ.
Следовательно, длина отрезка (АВ) в пространстве равняется длине гипотенузы прямоугольного треугольника, одним катетом которого является горизонтальная проекция (A1B1), а другим - разность длин горизонтально-проектирующих прямых (ВВ1 - АА1 = ВС).
На основании этого по комплексному чертежу отрезка общего положения можно определить его длину.
Разберем это на комплексном чертеже отрезка АВ общего положения, заданного двумя проекциями (фиг.210).
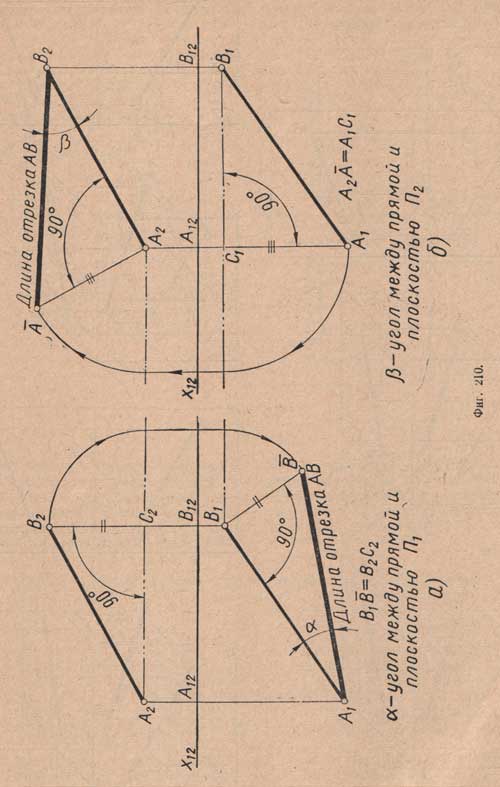
Определим катеты прямоугольного треугольника. Горизонтальную проекцию A1B1 принимаем за один катет. Отрезки A2A12 и В2В12 - это высоты, равные горизонтально - проектирующим прямым, разность которых В2С2 равна второму катету. Построим прямоугольный треугольник. Приняв за его основание горизонтальную проекцию А1В1, из точки В1 проводим к ней перпендикуляр; на нем от точки В1 откладываем отрезок В2С2, получим точку В. Точку В соединяем прямой с точкой A1 получаем прямоугольный треугольник А1В1B, гипотенуза которого А1В будет равна длине проектируемого отрезка АВ (фиг.210,а).
Это будет справедливо и для построения треугольника, если за основание его взять фронтальную проекцию A2В2 (фиг.210,б). Тогда гипотенуза АВ2 будет равна гипотенузе А1В1 (фиг.210,а), так как является натуральной величиной одного и того же отрезка.











