Способ вращения.

1. Вращение точки вокруг оси, перпендикулярной плоскости проекций. Дана ось i, перпендикулярная к плоскости проекций П₁, и точка А, вращающаяся вокруг нее в плоскости β, параллельной плоскости П₁ и одновременно перпендикулярной к оси вращения i (фиг.261).

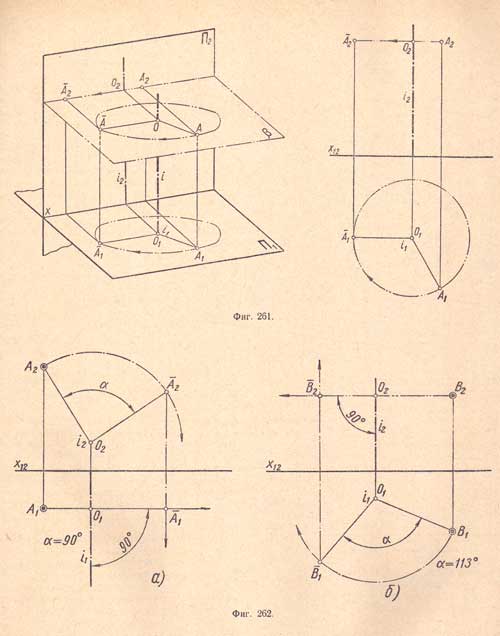
При вращении точка А перемещается по окружности в плоскости вращения β. Центр окружности является точкой пересечения оси вращения с плоскостью вращения и называется центром О вращения, а расстояние от точки А до центра вращения - радиусом вращения.
Траектория точки А на плоскость П₁ проектируется окружностью, а на плоскость П₂ - отрезком прямой, параллельным оси х₁₂.
Ось вращения будет перпендикулярна плоскости проекций П₂; траектория точки на плоскость П₂ будет проектироваться окружностью, а на плоскость П₁ - отрезком прямой, параллельным оси х₁₂. Отсюда общее правило, если точка вращается вокруг оси, перпендикулярной к плоскости проекций, то проекция точки на этой плоскости перемещается по окружности, а другая проекция - по прямой, перпендикулярной к проекции оси вращения (или параллельно оси проекций).
На (фиг.262) приведены два примера, характеризующие это общее правило.
Пример 1. Вращение точки A вокруг оси i, перпендикулярной к плоскости П₂ (фиг.262,а).
Пример 2. Вращение точки В вокруг оси i, перпендикулярной к плоскости П₁ (фиг.262,б).
2. Определение длины отрезка, формы и размеров плоской фигуры. Способом вращения можно определять длину отрезка, форму и размеры плоской фигуры.
Для того чтобы определить длину отрезка АВ, надо повернуть отрезок так, чтобы он расположился параллельно плоскости П₂ или плоскости П₁; тогда на соответствующей плоскости проекция отрезка будет равна его длине (фиг.263).

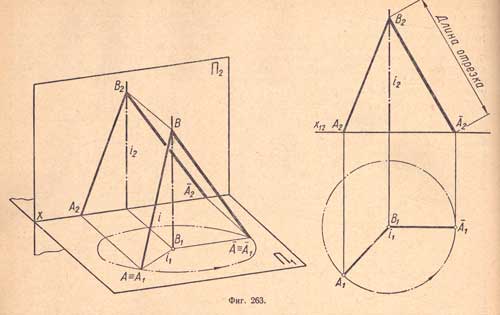
Для удобства построения ось вращения следует проводить через один из концов отрезка, например через точку В, тогда эта точка, находясь на оси вращения, не изменит своего положения и задача будет сводиться к вращению другого конца отрезка, т. е. точки А.
В данном примере ось вращения i перпендикулярна плоскости П₁ и проходит через точку В.
Другой конец A отрезка находится на плоскости П₁ отрезок повертывают так, чтобы он расположился параллельно плоскости П₂, т.е. занял положение фронтали; его горизонтальная проекция А₁В₁ не изменит своего размера и будет параллельна оси х₁₂. При помощи вертикальной линии связи находят фронтальную проекцию ‾А₂ - она лежит на оси х₁₂ - Соединив точки В₂ и ‾А₂ отрезком прямой, получают фронтальную проекцию В₂ ‾А₂ отрезка, равную его длине.
Если взять ось вращения, перпендикулярную к плоскости П₂, то получим тот же результат, но только тогда отрезок займет положение не фронтали, а горизонтали (фиг.264,а).

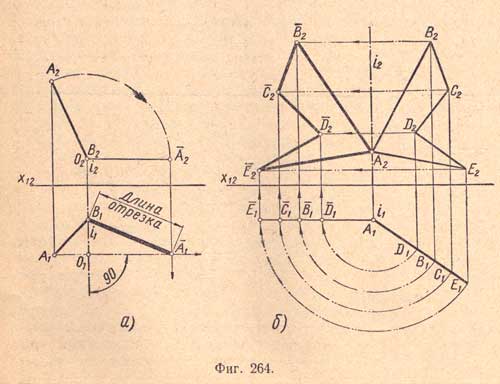
На (фиг.264,б) показано определение формы и размеров плоской фигуры ABCDE путем ее поворота из горизонтально-проектирующего положения во фронтальное.
Решение задачи сводится к вращению вершин данной фигуры вокруг оси i, перпендикулярной плоскости П₁ проходящей через точку А - вершину фигуры. Горизонтальная проекция фигуры, выявленная отрезком прямой, повернута так, что она стала параллельной оси х₁₂. При помощи вертикальных линий связи и горизонтальных прямых получаем новую фронталь. ную проекцию A₂ ‾B₂ ‾C₂ ‾D₂ ‾E₂ плоского пятиугольника, определяющую его форму и размеры.

Вращение плоскости вокруг ее следов.....