Задание плоскости на чертеже.
Изображение плоскости на комплексном чертеже, задание плоскости
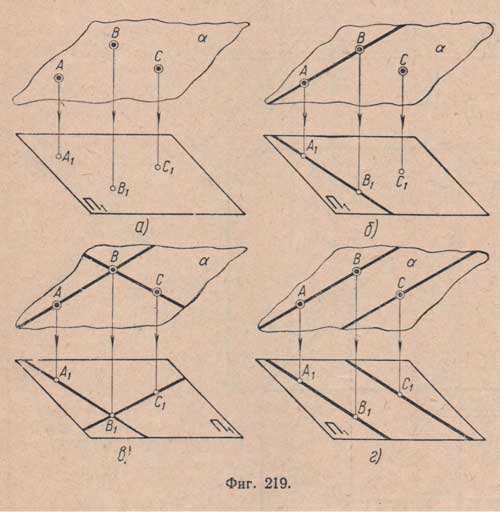
Плоскость в пространстве может быть определена:
а) тремя точками, не лежащими на одной прямой (фиг.219,а);
б) прямой и точкой, не лежащей на этой прямой (фиг.219,б);
в) двумя пересекающимися прямыми (фиг.219,в);
г) двумя параллельными прямыми (фиг.219,г).
Следовательно, на комплексном чертеже плоскость может быть задана проекциями трех точек: А, В и С (фиг.220,а). Если через две из трех данных точек, например А и В, провести прямую, то та же плоскость будет задана проекциями прямой АВ и точкой С в не ее (фиг.220,б).
Если через проекции этих трех точек А, В и С провести прямые, например из проекций точек А и С через проекцию точки В, то та же плоскость будет задана двумя пересекающимися прямыми (фиг.220,б). Наконец, если через проекции точек А и В провести прямую, а через проекции точки С вторую прямую, параллельную проекции АВ, то эта же плоскость будет задана проекциями двух параллельных прямых (фиг.220,г). Пусть на комплексном чертеже даны проекции трех точек А, В и С, требуется через них провести плоскость (фиг.221,а). Соединим их одноименные проекции прямыми, получим проекции плоской фигуры треугольника, лежащего в искомой плоскости. Отсюда следует, что плоскость может быть еще задана любой плоской фигурой (фиг.221,б).
Чаще всего на комплексном чертеже плоскости задаются двумя параллельными или пересекающимися прямыми, которые получаются в результате пересечения данной плоскости с плоскостями проекций.











