Эвольвента окружности.
Эвольвентой окружности называется плоская кривая — след движения любой точки А окружности при ее развертывании в одну сторону и одновременном выпрямлении (фиг.161).
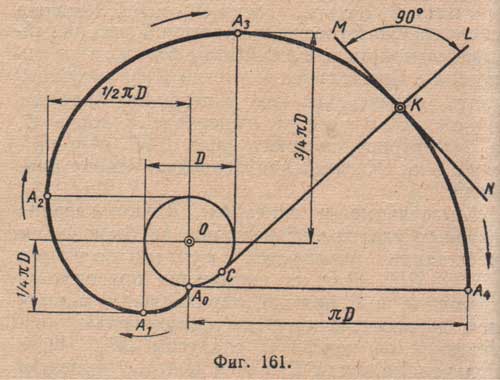
Шаг эвольвенты А0A4 равен длине окружности, т. е. ΠD. Линия CL, проходящая через любую точку К эвольвенты касательно к развертываемой окружности, называется нормалью эвольвенты. Прямая MN, проведенная через точку К перпендикулярно нормали, будет касательной эвольвенты.
1. Образование эвольвенты окружности. На (фиг.162) показано приспособление, при помощи которого можно легко уяснить образование эвольвенты окружности.
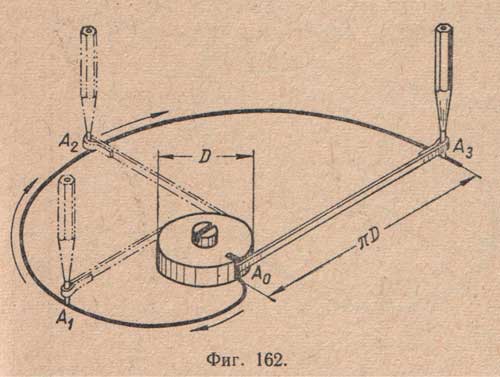
Вокруг неподвижного диска диаметром D навернута на один оборот тесьма, конец которой закреплен на боковой кромке диска, а на другом конце сделана петля. Если, натягивая тесьму вставленным в петлю карандашом, разматывать ее, то карандаш вычертит кривую - эвольвенту окружности, шаг которой равен nD окружности диска. В любом положении при таком развертывании тесьмы она будет каса-тельна к окружности диска.
Построение эвольвенты окружности.
Данную развертываемую окружность диаметром D (фиг.163,а) делят на произвольное число равных частей (для получения достаточно плавной кривой рекомендуется делить окружность не менее чем на 12 частей). Из каждой точки деления проводят касательную, направленную в одну и ту же сторону, например в противоположную движению часовой стрелки (или наоборот).
На первой касательной откладывают от точки касания 1/12 часть nD, на второй — 2/12; на третьей 3/12 и т. д., следовательно на двенадцатой касательной надо отложить 12/12 nD, т. е. nD. Проведя кривую по найденным на касательных конечным точкам, получают эвольвенту окружности (фиг.163,б).
На (фиг.164) показан пример применения эвольвенты окружности. Очертания боковых сторон профилей зубьев зубчатых колес обычно выполняют по эвольвенте.
Смотри также: Парабола.....











