Винт.

Винты в большинстве случаев имеют цилиндрическую форму. Витки винта получаются в результате перемещения вокруг цилиндра, по винтовым линиям, плоской фигуры (профиля), находящейся все время в плоскости, проходящей через ось вращения цилиндра. В зависимости от профиля винты могут иметь нарезки (резьбы): треугольные, прямоугольные, трапецеидальные и др. На (фиг.367,а) показано построение проекций витков цилиндрического винта, образованных движением профиля - прямоугольной трапеции ABCD.

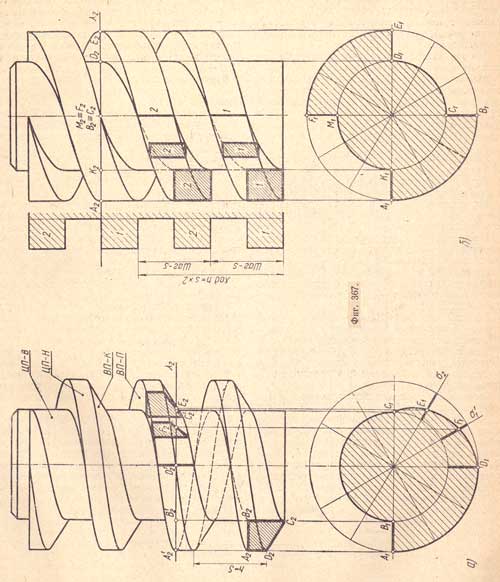
Заметим, что точки В₂ и С₂ профиля - трапеции - опишут винтовые линии на цилиндре меньшего диаметра, который назовем внутренним, а точки A₂ и D₂ - на цилиндре большего диаметра, который назовем внешним.
Стороны АВ и CD трапеции образуют винтовые поверхности.
Сторона ВС трапеции лежит на образующей внутреннего цилиндра.
Для получения фронтальной проекции следует построить по данному шагу S четыре винтовые линии, образованные вершинами прямоугольной трапеции, т. е. точками А, В, С, D, и соединить их в соответствующих местах касательными - прямыми вместо огибающих кривых.
В результате получим фронтальную проекцию одного витка.
Совокупность винтовых поверхностей витка с поверхностями наружного и внутреннего цилиндров образует поверхность винта.
В данном случае поверхность цилиндрического винта с правой трапецеидальной (упорной) резьбой ограничена: прямой (ВП - П) и косой (ВП - К) винтовыми поверхностями и двумя цилиндрическими поверхностями - одной наружной (ЦП - Н) и другой внутренней (ЦП - В).

Вместо горизонтальной проекции построено поперечное сечение винта горизонтальной плоскостью λ.
Контур фигуры сечения состоит из отрезка, двух дуг окружности и спирали Архимеда. Секущая плоскость пересекает прямую винтовую поверхность по отрезку прямой A₁В₁ цилиндрические поверхности - по дугам A₁D₁ и В₁С₁ и косую винтовую поверхность - по спирали Архимеда C₁D₁, точки F₁ и Е₁, которой определены при помощи дополнительных сечений горизонтально - проектирующими плоскостями σ' и σ² через ось вращения цилиндра. Этот винт называется однозаходным, так как он образован одним профилем трапеции, вершины которой перемещены на величину S винтовой линии и, следовательно, ход h однозаходного винта равен шагу s (h = s).
Для получения двухзаходного винта надо иметь два независимых витка.
На (фиг.367,б) показано построение двухзаходного винта с прямоугольной правой резьбой. В этом случае для образования винта взято два профиля - прямоугольника.
Ход у такого винта равен шагу, умноженному на число заходов: h = s x 2.
В практике обычно для определения числа заходов винта достаточно осмотреть торцовую поверхность и сосчитать на нем количество концов ниток.
Изображенное на (фиг.367,б) сечение горизонтальной плоскостью λ, показывает двухзаходность винта. Фигура горизонтального сечения ограничена четырьмя дугами и четырьмя отрезками прямых. Прямые получены от пересечения секущей плоскости с прямыми винтовыми поверхностями; дуги получены от пересечения секущей плоскости с наружной и внутренней цилиндрическими поверхностями.

Винтовые линии.....